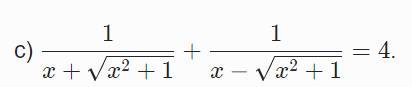\(\dfrac{1}{x+\sqrt{x^2+1}}+\dfrac{1}{x-\sqrt{x^2+1}}=4\)
\(\Leftrightarrow\dfrac{x-\sqrt{x^2+1}}{\left(x+\sqrt{x^2+1}\right)\left(x-\sqrt{x^2+1}\right)}+\dfrac{x+\sqrt{x^2+1}}{\left(x+\sqrt{x^2+1}\right)\left(x-\sqrt{x^2+1}\right)}=4\)
\(\Leftrightarrow\dfrac{x-\sqrt{x^2+1}-x+\sqrt{x^2+1}}{\left(x+\sqrt{x^2+1}\right)\left(x-\sqrt{x^2+1}\right)}=4\)
\(\Leftrightarrow-2x=4\left[x^2-\left(\sqrt{x^2+1}\right)^2\right]\)
\(\Leftrightarrow-2x=4\left(x^2-x^2+1\right)\)
\(\Leftrightarrow-2x=4\cdot1\)
\(\Leftrightarrow-2x=4\)
\(\Leftrightarrow x=\dfrac{4}{-2}\)
\(\Leftrightarrow x=-2\)
=>\(\dfrac{x-\sqrt{x^2+1}}{x^2-x^2-1}+\dfrac{x+\sqrt{x^2+1}}{x^2-x^2-1}=4\)
=>\(-x+\sqrt{x^2+1}-x-\sqrt{x^2+1}=4\)
=>-2x=4
=>x=-2