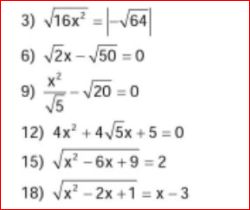3) \(\Leftrightarrow4\left|x\right|=8\Leftrightarrow\left|x\right|=2\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
6) \(\Leftrightarrow x=\sqrt{50}:\sqrt{2}\Leftrightarrow x=5\)
9) \(\Leftrightarrow x^2=\sqrt{20}.\sqrt{5}\Leftrightarrow x^2=10\Leftrightarrow x=\pm\sqrt{10}\)
12) \(\Leftrightarrow\left(2x+\sqrt{5}\right)^2=0\)
\(\Leftrightarrow2x+\sqrt{5}=0\Leftrightarrow x=-\dfrac{\sqrt{5}}{2}\)
15) \(\Leftrightarrow\sqrt{\left(x-3\right)^2}=2\Leftrightarrow\left|x-3\right|=2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=2\\x-3=-2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
18) \(ĐK:x\ge3\)
\(\Leftrightarrow\sqrt{\left(x-1\right)^2}=x-3\Leftrightarrow\left|x-1\right|=x-3\)
\(\Leftrightarrow x-1=x-3\left(do.x\ge3\right)\Leftrightarrow-1=-3\left(VLý\right)\)
Vậy \(S=\varnothing\)
20) \(ĐK:x\ge1\)
\(\Leftrightarrow6\sqrt{x-1}-3\sqrt{x-1}-2\sqrt{x-1}+\sqrt{x-1}=16\)
\(\Leftrightarrow2\sqrt{x-1}=6\Leftrightarrow\sqrt{x-1}=3\Leftrightarrow x-1=9\Leftrightarrow x=10\left(tm\right)\)