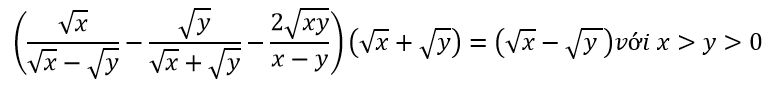\(\left(\dfrac{\sqrt{x}}{\sqrt{x}-\sqrt{y}}-\dfrac{\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\dfrac{2\sqrt{xy}}{x-y}\right)\left(\sqrt{x}+\sqrt{y}\right)=\dfrac{\sqrt{x}\left(\sqrt{x}+\sqrt{y}\right)-\sqrt{y}\left(\sqrt{x}-\sqrt{y}\right)-2\sqrt{xy}}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}.\left(\sqrt{x}+\sqrt{y}\right)\)\(=\dfrac{x+\sqrt{xy}-\sqrt{xy}+y-2\sqrt{xy}}{\sqrt{x}-\sqrt{y}}=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\sqrt{x}-\sqrt{y}}=\sqrt{x}-\sqrt{y}\)
Ta có: \(\left(\dfrac{\sqrt{x}}{\sqrt{x}-\sqrt{y}}-\dfrac{\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\dfrac{2\sqrt{xy}}{x-y}\right)\cdot\left(\sqrt{x}+\sqrt{y}\right)\)
\(=\dfrac{x+\sqrt{xy}-\sqrt{xy}+y-2\sqrt{xy}}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}\cdot\left(\sqrt{x}+\sqrt{y}\right)\)
\(=\sqrt{x}-\sqrt{y}\)