Nêu điều kiện để \(x\) là căn bậc hai số học của số a không âm. Cho ví dụ ?
Chứng minh \(\sqrt{a^2}=\left|a\right|\) với mọi số a
Biểu thức A phải thỏa mãn điều kiện gì để \(\sqrt{A}\) xác định ?
\(\sqrt{ }\)A xác định khi A > 0 hay nói cách khác : điều kiện xác định của căn bậc hai là biểu thức lấy căn không âm.
Trả lời bởi Lưu Hạ VyPhát biểu và chứng minh định lí về mối liên hệ giữa phép nhân và phép khai phương. Cho ví dụ ?
Phát biểu và chứng minh định lí về mối liên hệ giữa phép chia và phép khai phương. Cho ví dụ ?
Tìm giá trị các biểu thức sau bằng cách biến đổi rút gọn thích hợp :
a) \(\sqrt{\dfrac{25}{81}.\dfrac{16}{49}.\dfrac{196}{9}}\)
b) \(\sqrt{3\dfrac{1}{16}.2\dfrac{14}{25}.2\dfrac{34}{81}}\)
c) \(\dfrac{\sqrt{640}.\sqrt{34,3}}{\sqrt{567}}\)
d) \(\sqrt{21,6}.\sqrt{810}.\sqrt{11^2-5^2}\)
a) \(\sqrt{\dfrac{25}{81}.\dfrac{16}{49}.\dfrac{196}{9}}=\sqrt{\dfrac{25}{81}}.\sqrt{\dfrac{16}{49}}.\sqrt{\dfrac{196}{9}}=\dfrac{5}{9}.\dfrac{4}{7}.\dfrac{14}{3}=\dfrac{40}{27}\)
b) \(\sqrt{3\dfrac{1}{16}.2\dfrac{14}{25}.2\dfrac{34}{81}}=\sqrt{\dfrac{49}{16}.\dfrac{64}{25}.\dfrac{196}{81}}=\sqrt{\dfrac{49}{16}}.\sqrt{\dfrac{64}{25}}.\sqrt{\dfrac{196}{81}}=\dfrac{7}{4}.\dfrac{8}{5}.\dfrac{14}{9}=\dfrac{196}{45}\)
c) \(\dfrac{\sqrt{640}.\sqrt{34,3}}{\sqrt{567}}=\sqrt{\dfrac{640.34,3}{567}}=\sqrt{\dfrac{64.49}{81}}=\dfrac{\sqrt{64}.\sqrt{49}}{\sqrt{81}}=\dfrac{8.7}{9}=\dfrac{56}{9}\)
d) \(\sqrt{21,6}.\sqrt{810}.\sqrt{11^2-5^2}=\sqrt{21,6.810.\left(11^2-5^2\right)}=\sqrt{216.81.\left(11+5\right)\left(11-5\right)}=\sqrt{36^2.9^2.4^2}=36.9.4=1296\)
Trả lời bởi Mysterious Person
Rút gọn các biểu thức sau :
a) \(\left(\sqrt{8}-3\sqrt{2}+\sqrt{10}\right)\sqrt{2}-\sqrt{5}\)
b) \(0,2\sqrt{\left(-10\right)^2.3}+2\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}\)
c) \(\left(\dfrac{1}{2}\sqrt{\dfrac{1}{2}}-\dfrac{3}{2}\sqrt{2}+\dfrac{4}{5}\sqrt{200}\right):\dfrac{1}{8}\)
d) \(2\sqrt{\left(\sqrt{2}-3\right)^2}+\sqrt{2.\left(-3\right)^2}-5\sqrt{\left(-1\right)^4}\)
Phân tích thành nhân tử ( với các số x, y, a, b không âm và \(a\ge b\))
a) \(xy-y\sqrt{x}+\sqrt{x}-1\)
b) \(\sqrt{ax}-\sqrt{by}+\sqrt{bx}-\sqrt{ay}\)
c) \(\sqrt{a+b}+\sqrt{a^2-b^2}\)
d) \(12-\sqrt{x}-x\)
Rút gọn rồi tính giá trị của các biểu thức sau :
a) \(\sqrt{-9a}-\sqrt{9+12x+4a^2}\) tại \(a=-9\)
b) \(1+\dfrac{3m}{m-2}\sqrt{m^2-4m+4}\) tại \(m=1,5\)
c) \(\sqrt{1-10a+25a^2}-4a\) tại \(a=\sqrt{2}\)
d) \(4x-\sqrt{9x^2+6x+1}\) tại \(x=-\sqrt{3}\)
a) \(\sqrt{-9a}-\sqrt{9+12a+4a^2}\) \(=\sqrt{9.\left(-a\right)}-\sqrt{\left(3+2a\right)^2}=3\sqrt{-a}-\left|3+2a\right|\)
\(=3\sqrt{9}-\left|3+2\left(-9\right)\right|=3.3-15=-6\)
b) \(1+\dfrac{3m}{m-2}\sqrt{m^2-4x+4}=1+\dfrac{3m}{m-2}\sqrt{\left(m-2\right)^2}=1+\dfrac{3m\left|m-2\right|}{m-2}\)
\(=\left\{{}\begin{matrix}1+3m\left(nếu\left(m-2\right)>0\right)\\1-3m\left(nến\left(m-2\right)< 0\right)\end{matrix}\right.\) \(=\left\{{}\begin{matrix}1+3m\left(nếu\left(m>2\right)\right)\\1-3m\left(nếu\left(m< 2\right)\right)\end{matrix}\right.\)
ta có : \(m=1,5< 2\) vậy giá trị của biểu thức tại m = 1,5 là \(1-3m\) = \(1-3.1,5=-3,5\)
c) \(\sqrt{1-10a+25a^2}-4a=\sqrt{\left(1-5a\right)^2}-4a=\left|1-5a\right|-4a\)
\(=\left\{{}\begin{matrix}1-9a\left(nếu\left(1-5a\right)\ge0\right)\\a-1\left(nếu\left(1-5a\right)< 0\right)\end{matrix}\right.\) \(=\left\{{}\begin{matrix}1-9a\left(nếu\left(a\le\dfrac{1}{5}\right)\right)\\a-1\left(nếu\left(a>\dfrac{1}{5}\right)\right)\end{matrix}\right.\)
ta có : \(a=\sqrt{2}>\dfrac{1}{5}\) vậy giá trị của biểu thức tại \(a=\sqrt{2}\) là a - 1 = \(\sqrt{2}-1\)
d) \(4x-\sqrt{9x^2+6x+1}=4x-\sqrt{\left(3x+1\right)^2}=4x-\left|3x+1\right|\)
\(=\left\{{}\begin{matrix}x-1\left(nếu\left(x\ge-\dfrac{1}{3}\right)\right)\\7x+1\left(nếu\left(x< -\dfrac{1}{3}\right)\right)\end{matrix}\right.\)
ta có : \(x=-\sqrt{3}< -\dfrac{1}{3}\) vậy giá trị của biểu thức tại \(x=-\sqrt{3}\) là \(7.\left(-\sqrt{3}\right)+1=1-7\sqrt{3}\)
Trả lời bởi Mysterious Person
Tìm \(x\), biết :
a) \(\sqrt{\left(2x-1\right)^2}=3\)
b) \(\dfrac{5}{3}\sqrt{15x}-\sqrt{15x}-2=\dfrac{1}{3}\sqrt{15x}\)
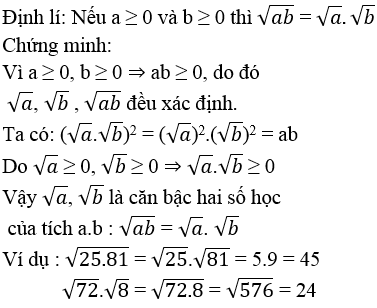
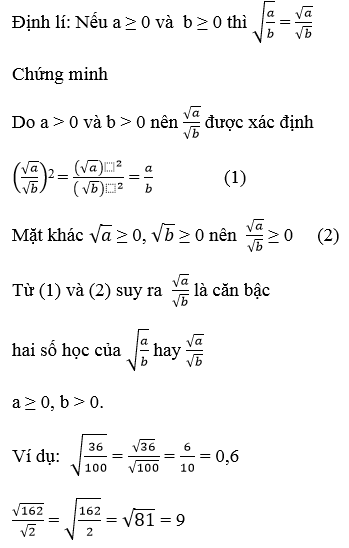
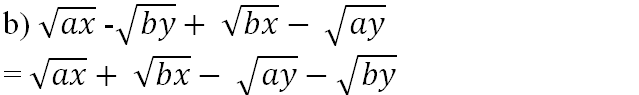
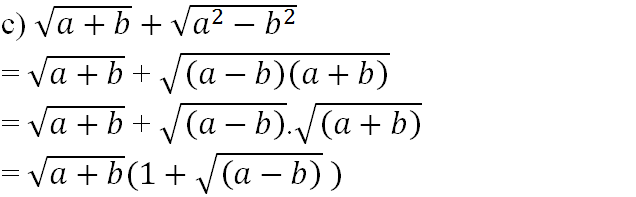
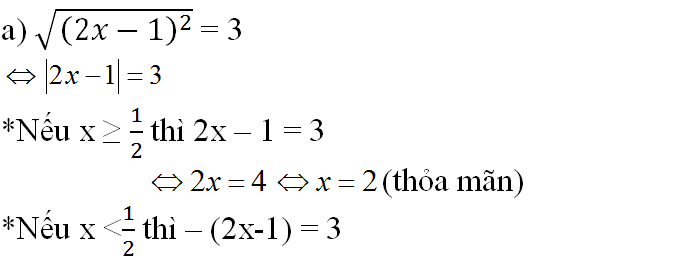
Để x là căn bậc hai số học của số a không âm là x \(\ge\) a và x2 = a.
Ví dụ 2 là căn bậc hai số học của 4 vì 2 > 0 và 22 = 4.
Trả lời bởi Lưu Hạ Vy