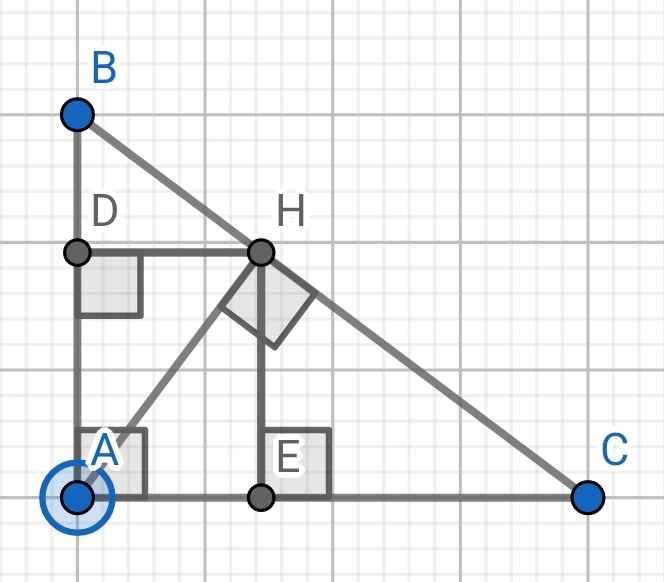
a) Xét hai tam giác vuông: ∆HAC và ∆ABC có:
∠C chung
∆HAC ∽ ∆ABC (g-g)
b) Xét hai tam giác vuông: ∆AHB và ∆ADH có:
∠A chung
⇒ ∆AHB ∽ ∆ADH (g-g)
⇒ AH/AD = AB/AH
⇒ AH.AH = AD.AB
Hay AH² = AD.AB (1)
c) Xét hai tam giác vuông: ∆AHC và ∆AEH có:
∠A chung
⇒ ∆AHC ∽ ∆AEH (g-g)
⇒ AH/AE = AC/AH
⇒ AH.AH = AE.AC
Hay AH² = AE.AC (2)
Từ (1) và (2) ⇒ AD.AB = AE.AC
a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
góc C chung
=>ΔHAC đồng dạng với ΔABC
b: ΔAHB vuông tại H
mà HD là đường cao
nên AH^2=AD*AB
c: ΔACH vuông tại H có HE là đường cao
nên AE*AC=AH^2=AD*AB