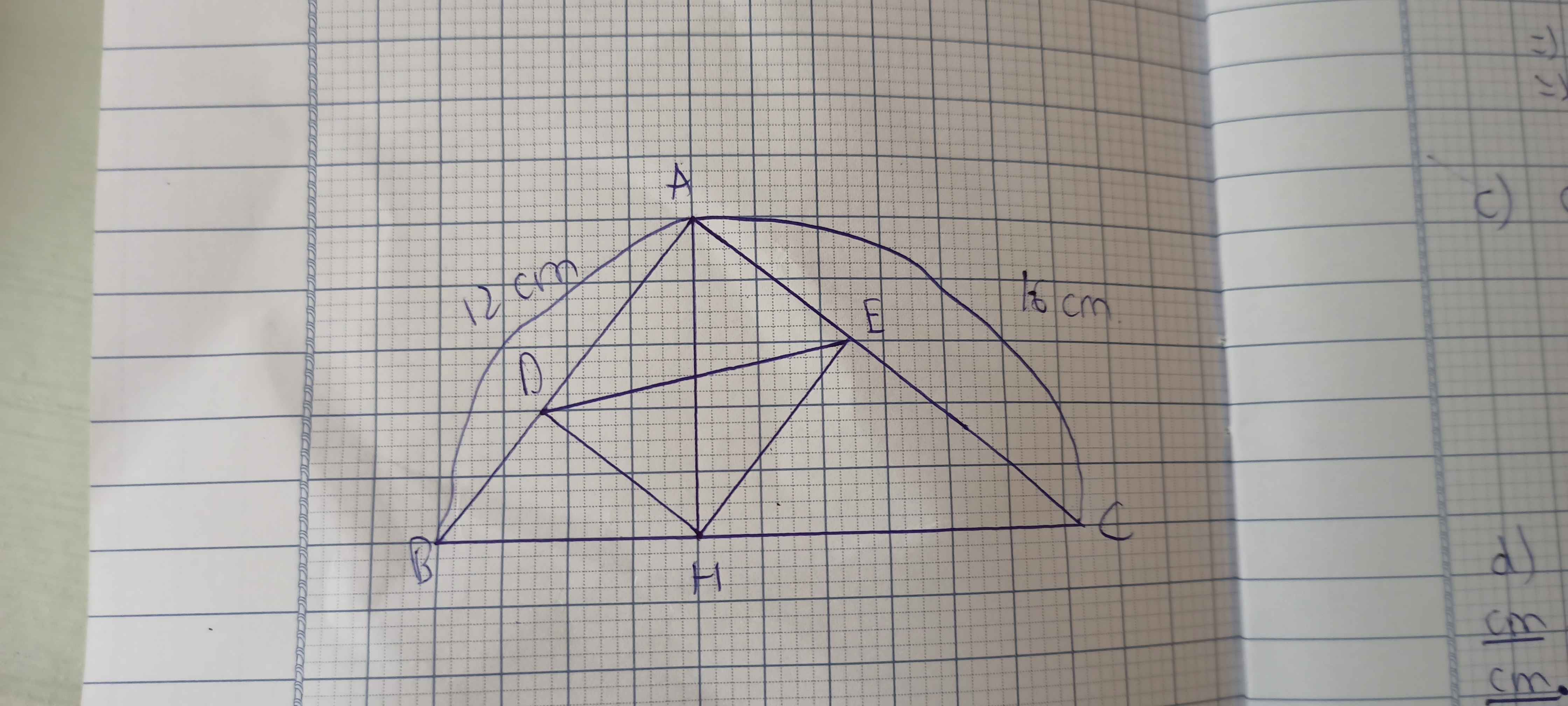
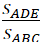Hình tự vẽ nha bạn
a. Xét △HAC và △ABC ta có
∠ C chung
∠ A = ∠ H ( = \(90^o\) )
Vậy △HAC∼△ABC \(\left(g-g\right)\)
a) Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{ACB}\) chung
Do đó: ΔHAC\(\sim\)ΔABC(g-g)
b) Xét ΔAHD vuông tại D và ΔABH vuông tại H có
\(\widehat{HAD}\) chung
Do đó: ΔAHD\(\sim\)ΔABH(g-g)
Suy ra: \(\dfrac{AH}{AB}=\dfrac{AD}{AH}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AH^2=AD\cdot AB\)(đpcm)
c) Xét ΔAHE vuông tại E và ΔACH vuông tại H có
\(\widehat{HAE}\) chung
Do đó: ΔAHE\(\sim\)ΔACH(g-g)
Suy ra: \(\dfrac{AH}{AC}=\dfrac{AE}{AH}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AH^2=AE\cdot AC\)
mà \(AH^2=AD\cdot AB\)(cmt)
nên \(AD\cdot AB=AE\cdot AC\)