Cho \(\Delta ABC\) nhọn ( AB < AC ). Tia phân giác của\(\widehat{BAC}\) cắt BC tại D. Trên AC lầy điểm E sao cho AE = AB.
a) \(\Delta ABD\) = \(\Delta AED\) và \(\widehat{ABD}\) = \(\widehat{AED}\)
b) Gọi F là giao điểm của AB và ED. Chứng minh: \(\Delta DBF\) = \(\Delta DEC\)
c) Đường thẳng qua E song song với AD cắt BC tại M. Gọi N là trung điểm của FC. Chứng minh: DN // EM
- Vẽ hình giúp mình!!
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
=>\(\widehat{ABD}=\widehat{AED}\)
b: Ta có: \(\widehat{ABD}+\widehat{DBF}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)
nên \(\widehat{DBF}=\widehat{CED}\)
Ta có: ΔABD=ΔAED
=>DB=DE
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)(đối đỉnh)
Do đó: ΔDBF=ΔDEC
c: Ta có: ΔDBF=ΔDEC
=>BF=EC
Ta có: AB+BF=AF
AE+EC=AC
mà AB=AE và BF=EC
nên AF=AC
=>A nằm trên đường trung trực của CF(1)
Ta có: ΔDBF=ΔDEC
=>DF=DC
=>D nằm trên đường trung trực của CF(2)
Ta có: NF=NC
=>N nằm trên đường trung trực của CF(3)
Từ (1),(2),(3) suy ra A,D,N thẳng hàng
=>AN//EM
=>DN//EM
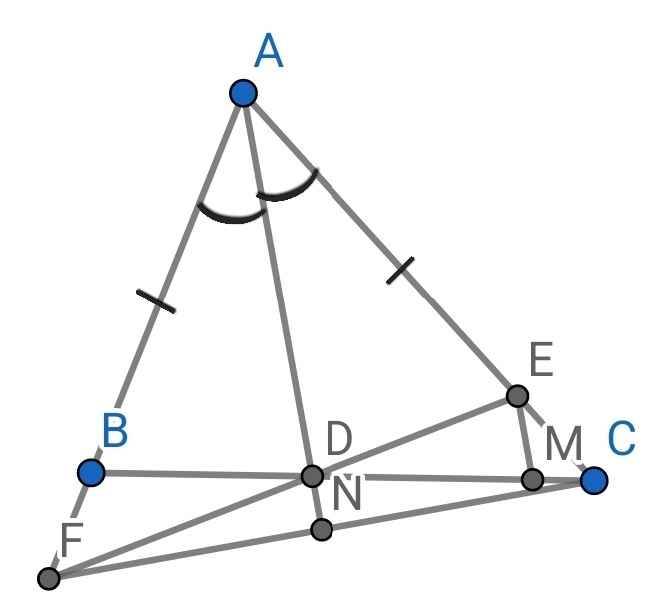
a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
⇒ ∠BAD = ∠EAD
Xét ∆ABD và ∆AED có:
AD là cạnh chung
∠BAD = ∠EAD (cmt)
AB = AE (gt)
⇒ ∆ABD = ∆AED (c-g-c)
⇒ ∠ABD = ∠AED (hai góc tương ứng)
b) Ta có:
∠FBD + ∠ABD = 180⁰ (kề bù)
∠CED + ∠AED = 180⁰ (kề bù)
Mà ∠ABD = ∠AED (cmt)
⇒ ∠FBD = ∠CED
Do ∆ABD = ∆AED (cmt)
⇒ BD = ED (hai cạnh tương ứng)
Xét ∆DBF và ∆DEC có:
∠FBD = ∠CED (cmt)
BD = ED (cmt)
∠BDF = ∠CDE (đối đỉnh)
⇒ ∆DBF = ∆DEC (g-c-g)
c) Do ∆DBF = ∆DEC (cmt)
⇒ BF = EC (hai cạnh tương ứng)
Ta có:
AF = AB + BF
AC = AE + EC
Mà AB = AE (gt)
BF = EC (cmt)
⇒ AF = AC
⇒ ∆AFC cân tại A
Mà N là trung điểm của FC (gt)
⇒ AN là đường trung tuyến của ∆AFC
⇒ AN cũng là đường phân giác của ∆AFC
⇒ AN là tia phân giác của ∠ABC
⇒ A, N, D thẳng hàng
Mà AD // EM (gt)
⇒ AN // EM



