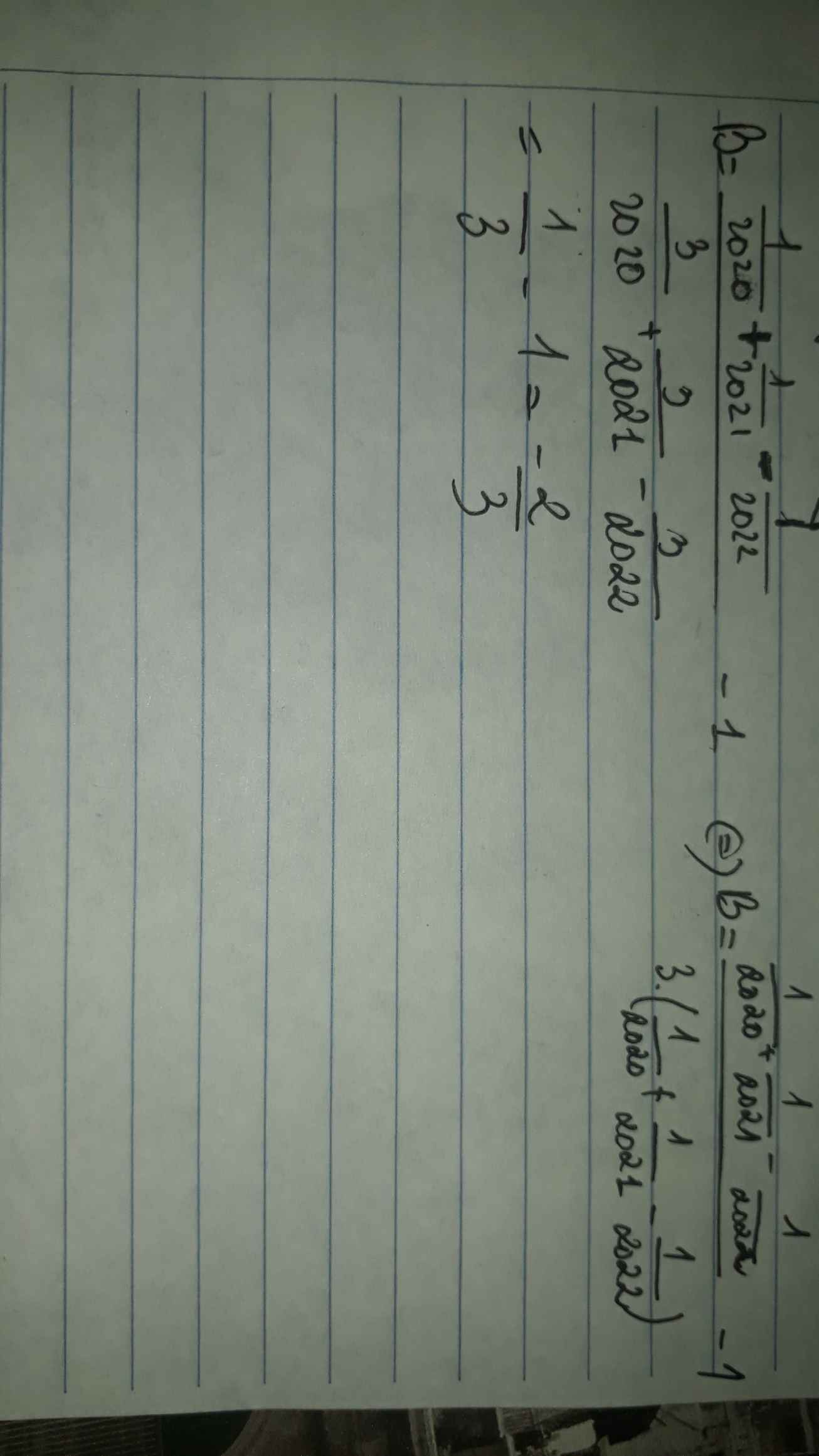\(B=\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{\dfrac{3}{2020}+\dfrac{3}{2021}-\dfrac{3}{2022}}-1=\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{3\left(\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}\right)}-1=\dfrac{1}{3}-1=-\dfrac{2}{3}\)
\(B=\dfrac{\dfrac{1}{2021}+\dfrac{1}{2021}-\dfrac{1}{2022}}{\dfrac{3}{2020}+\dfrac{3}{2021}-\dfrac{3}{2022}}-1=\dfrac{\dfrac{1}{2021}+\dfrac{1}{2021}-\dfrac{1}{2022}}{3\left(\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}\right)}-1=\dfrac{1}{3}-1=\dfrac{1}{3}-\dfrac{3}{3}=-\dfrac{2}{3}\)
\(B=\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{\dfrac{3}{2020}+\dfrac{3}{2021}-\dfrac{3}{2022}}-1\)
\(=\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{3\left(\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}\right)}-1\)
\(=3-1=2\)
B=\(\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{\dfrac{3}{2020}+\dfrac{3}{2021}-\dfrac{3}{2022}}-1=\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{3.\left(\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}\right)}-1=\dfrac{1}{3}-1=\dfrac{-2}{3}\)
\(B=\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{\dfrac{3}{2020}+\dfrac{3}{2021}-\dfrac{3}{2022}}-1\)
\(=\dfrac{1}{3}-1\)
\(=-\dfrac{2}{3}\)