Rút gọn các biểu thức sau :
a) \(\left(x+3\right)\left(x^2-3x+9\right)-\left(54+x^3\right)\)
b) \(\left(2x+y\right)\left(4x^2-2xy+y^2\right)-\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
Chứng minh rằng :
a) \(a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)\)
b) \(a^3-b^3=\left(a-b\right)^3+3ab\left(a-b\right)\)
Áp dụng :
Tính \(a^3+b^3\), biết \(a.b=6\) và \(a+b=-5\)
a) a3 + b3 = (a + b)3 – 3ab(a + b)
Thực hiện vế phải:
(a + b)3 – 3ab(a + b) = a3 + 3a2b+ 3ab2 + b3 – 3a2b – 3ab2
= a3 + b3
Vậy a3 + b3 = (a + b)3 – 3ab(a + b)
b) a3 – b3 = (a – b)3 + 3ab(a – b)
Thực hiện vế phải:
(a – b)3 + 3ab(a – b) = a3 - 3a2b+ 3ab2 - b3 + 3a2b – 3ab2
= a3 – b3
Vậy a3 – b3 = (a – b)3 + 3ab(a – b)
Áp dụng:
Với ab = 6, a + b = -5, ta được:
a3 + b3 = (a + b)3 – 3ab(a + b) = (-5)3 - 3 . 6 . (-5)
= -53 + 3 . 6 . 5 = -125 + 90 = -35.
Điền các đơn thức thích hợp vào ô trống :
a) \(\left(3x+y\right)\left(.....-......+......\right)=27x^3+y^3\)
b) \(\left(2x-.....\right)\left(.....+10x+......\right)=8x^3-125\)
a) Ta có: 27\(x^3\)+ y\(^3\) = (3x)\(^3\) + y\(^3\)= (3x + y)[(3x)\(^2\) – 3x . y + y\(^2\)] = (3x + y)(9x\(^2\) – 3xy + y\(^2\))
Nên: (3x + y) (9x\(^2\) – 3xy + y\(^2\)) = 27x\(^3\) + y\(^3\)
b) Ta có: 8x\(^3\) – 125 = (2x)\(^3\) – 53= (2x – 5)[(2x)\(^2\) + 2x . 5 + 5\(^2\)]
= (2x – 5)(4x\(^2\) + 10x + 25)
Nên:(2x – 5)(4x\(^2\) + 10x + 25)= 8x\(^3\) – 125
Tính :
a) \(\left(2+xy\right)^2\)
b) \(\left(5-3x\right)^2\)
c) \(\left(5-x^2\right)\left(5+x^2\right)\)
d) \(\left(5x-1\right)^3\)
e) \(\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
f) \(\left(x+3\right)\left(x^2-3x+9\right)\)
Bài giải:
a) (2 + xy)2 = 22 + 2 . 2 . xy + (xy)2 = 4 + 4xy + x2y2
b) (5 – 3x)2= 52 – 2 . 5 . 3x + (3x)2 = 25 – 30x + 9x2
c) (5 – x2)(5 + x2) = 52 – (x2)2 = 25 – x4
d) (5x – 1)3 = (5x)3 – 3 . (5x)2. 1 + 3 . 5x . 12 – 13 = 125x3 – 75x2 + 15x – 1
e) (2x – y)(4x2 + 2xy + y2) = (2x – y)[(2x)2 + 2x . y + y2] = (2x)3 – y3 = 8x3 – y3
f) (x + 3)(x2 – 3x + 9) = (x + 3)(x2 – 3x + 32) = x3 + 33 = x3 + 27.
Trả lời bởi Tuyết Nhi MelodyRút gọn các biểu thức sau :
a) \(\left(a+b\right)^2-\left(a-b\right)^2\)
b) \(\left(a+b\right)^3-\left(a-b\right)^3-2b^3\)
c) \(\left(x+y+z\right)^2-2\left(x+y+z\right)\left(x+y\right)+\left(x+y\right)^2\)
Bài giải:
a) (a + b)2 – (a – b)2 = (a2 + 2ab + b2) – (a2 – 2ab + b2)
= a2 + 2ab + b2 – a2 + 2ab - b2 = 4ab
Hoặc (a + b)2 – (a – b)2 = [(a + b) + (a – b)][(a + b) – (a – b)]
= (a + b + a – b)(a + b – a + b)
= 2a . 2b = 4ab
b) (a + b)3 – (a – b)3 – 2b3
= (a3 + 3a2b + 3ab2 + b3) – (a3 – 3a2b + 3ab2 – b3) – 2b3
= a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b - 3ab2 + b3 – 2b3
= 6a2b
Hoặc (a + b)3 – (a – b)3 – 2b3 = [(a + b)3 – (a – b)3] – 2b3
= [(a + b) – (a – b)][(a + b)2 + (a + b)(a – b) + (a – b)2] – 2b3
= (a + b – a + b)(a2 + 2ab + b2 + a2 – b2 + a2 – 2ab + b2) – 2b3
= 2b . (3a2 + b2) – 2b3 = 6a2b + 2b3 – 2b3 = 6a2b
c) (x + y + z)2 – 2(x + y + z)(x + y) + (x + y)2
= x2 + y2 + z2+ 2xy + 2yz + 2xz – 2(x2 + xy + yx + y2 + zx + zy) + x2 + 2xy + y2
= 2x2 + 2y2 + z2 + 4xy + 2yz + 2xz – 2x2 – 4xy – 2y2 – 2xz – 2yz = z2
Trả lời bởi Tuyết Nhi MelodyTính nhanh :
a) \(34^2+66^2+68.66\)
b) \(74^2+24^2-48.74\)
Bài giải:
a) 342 + 662 + 68 . 66 = 342 + 2 . 34 . 66 + 662 = (34 + 66)2 = 1002 = 10000.
b) 742 + 242 – 48 . 74 = 742 - 2 . 74 . 24 + 242 = (74 - 24)2
=502 =2500
Trả lời bởi Tuyết Nhi MelodyTính giá trị của biểu thức :
a) \(x^2+4x+4\) tại \(x=98\)
b) \(x^3+3x^2+3x+1\) tại \(x=99\)
Bài giải:
a) x2 + 4x + 4 = x2 + 2 . x . 2 + 22 = (x+ 2)2
Với x = 98: (98+ 2)2 =1002 = 10000
b) x3 + 3x2 + 3x + 1 = x3 + 3 . 1 . x2 + 3 . x .12+ 13 = (x + 1)3
Với x = 99: (99+ 1)3 = 1003 = 1000000
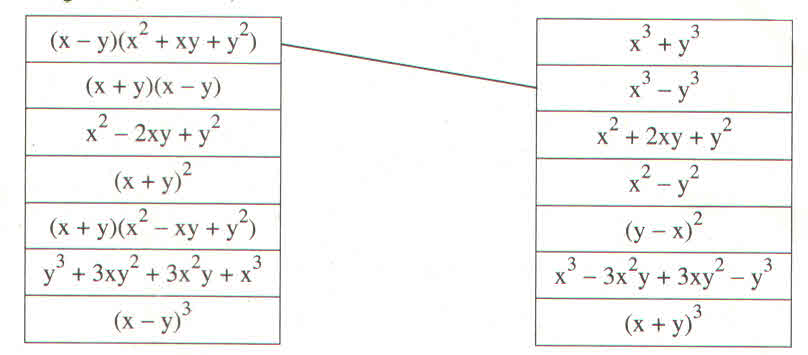
Trả lời bởi Tuyết Nhi MelodyNối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức (theo mẫu) :
Chứng minh các đẳng thức sau :
a) \(\left(a-b\right)^3=-\left(b-a\right)^3\)
b) \(\left(-a-b\right)^2=\left(a+b\right)^2\)
a) (a – b)3 = -(b – a)3
Biến đổi vế phải thành vế trái:
-(b – a)3= -(b3 – 3b2a + 3ba2 – a3) = - b3 + 3b2a - 3ba2 + a3
= a3 – 3a2b + 3ab2 – b3 = (a – b)3
Sử dụng tính chất hai số đối nhau:
(a – b)3 = [(-1)(b – a)]3 = (-1)3(b – a)3 = -13 . (b – a)3 = - (b – a)3
b) (- a – b)2 = (a + b)2
Biến đổi vế trái thành vế phải:
(- a – b)2 = [(-a) + (-b)]2
= (-a)2 +2 . (-a) . (-b) + (-b)2
= a2 + 2ab + b2 = (a + b)2
Sử dụng tính chất hai số đối nhau:
(-a – b)2 = [(-1) . (a + b)]2 = (-1)2 . (a + b)2 = 1 . (a + b)2 = (a + b)2
a) (x + 3)(x2 – 3x + 9) – (54 + x3) = (x + 3)(x2 – 3x + 32 ) - (54 + x3)
= x3 + 33 - (54 + x3)
= x3 + 27 - 54 - x3
= -27
b) (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)
= (2x + y)[(2x)2 – 2 . x . y + y2] – (2x – y)(2x)2 + 2 . x . y + y2]
= [(2x)3 + y3]- [(2x)3 - y3]
Trả lời bởi Trần Thị Bích Trâm= (2x)3 + y3- (2x)3 + y3= 2y3