Cho đường tròn (O;R) đường kính AB, tia tiếp tuyến Ax. Trên tia Ax lấy điểm M sao cho \(AM=R\sqrt{3}\). Vẽ tiếp tuyến MC (C là tiếp điểm). Đường thẳng vuông góc với AB tại O cắt BC tại D.
Khẳng định nào dưới đây là sai?
OM // BD. Tứ giác MDOA là hình chữ nhật. Tứ giác MDBO là hình bình hành. MO là tia phân giác của \(\widehat{AMD}\). Hướng dẫn giải: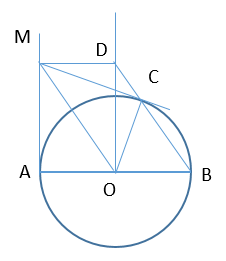
Có \(\)\(\widehat{ABC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\).
\(\widehat{AOM}=\dfrac{1}{2}\widehat{AOC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\).
Suy ra: \(\widehat{ABC}=\widehat{AOM}\).
Suy ra: OM // BC.
\(\Delta MAO=\Delta DOB\left(c.g.c\right)\) nên OM = BD.
Suy ra tứ giác OMDB là hình bình hành.
Suy ra MD = OB = OA.
Xét tứ giác MDOA có MD = OA và MA = DO nên là hình bình hành .
Hơn nữa \(\widehat{OAM}=90^o\) nên tứ giác MDOA là hình chữ nhật.
