Bài 3: Góc nội tiếp

Cho đường tròn (O) và hai dây AB, AC bằng nhau. Qua A vẽ một cát tuyến cắt dây BC ở D và cắt (O) ở E.
Khẳng định nào dưới đây là sai?​

\(AB^2=AD.AE\). Nếu \(\widehat{A}=40^o\) thì \(\widehat{AEB}=70^o\). Nếu tam giác ABC có \(\widehat{A}=60^o\) thì tam giác BDE đều. \(\Delta ABD\sim\Delta AEB\). Hướng dẫn giải:

​
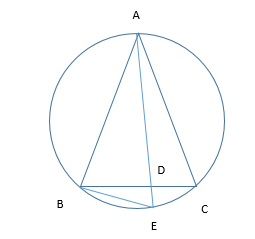
Có \(\left\{{}\begin{matrix}\widehat{AEB}=\dfrac{1}{2}\stackrel\frown{AB}\\\widehat{ABC}=\dfrac{1}{2}\stackrel\frown{AC}\\\stackrel\frown{AB}=\stackrel\frown{AC}\end{matrix}\right.\)  nên \(\widehat{AEB}=\widehat{ABC}\).
Suy ra: \(\Delta ADB\sim\Delta ABE\left(g.g\right)\).
Suy ra: \(\dfrac{AD}{AB}=\dfrac{AB}{AE}\)\(\Leftrightarrow AB^2=AD.AE\).
\(\widehat{BAC}=40^o\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^o-40^o}{2}=70^o\).