Tứ giác

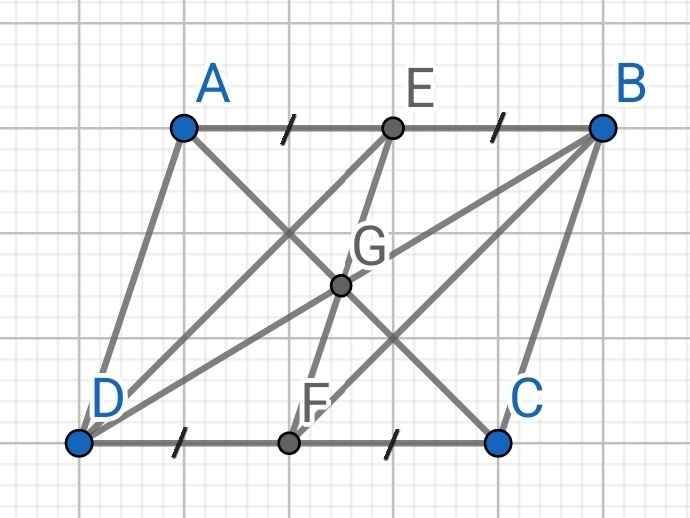 a) Do ABCD là hình bình hành (gt)

⇒ AB // CD

⇒ BE // DF

Do ABCD là hình bình hành

⇒ AB = CD (1)

Ta có:

E là trung điểm của AB (gt)

⇒ BE = AB : 2 (2)

F là trung điểm của CD (gt)

⇒ DF = CD : 2 (3)

Từ (1), (2) và (3) ⇒ BE = DF

Tứ giác BFDE có:

BE // DF (cmt)

BE = DF (cmt)

⇒ BFDE là hình bình hành

b) Gọi G là trung điểm của AC

Do ABCD là hình bình hành (gt)

⇒ G là trung điểm của AC và BD (4)

Do BFDE là hình bình hành (cmt)

G là trung điểm của BD (cmt)

⇒ G là trung điểm của EF (5)

Từ (4) và (5) ⇒ AC, BD, EF cắt nhau tại G

a: Xét tứ giác ANDM có

\(\widehat{AND}=\widehat{AMD}=\widehat{MAN}=90^0\)

=>ANDM là hình chữ nhật

b: Xét ΔABC có

D là trung điểm của CB

DN//AB

Do đó: N là trung điểm của AC

Xét tứ giác ADCEcó

N là trung điểm chung của AC và DE

=>ADCE là hình bình hành

Hình bình hành ADCE có AC\(\perp\)DE

nên ADCE là hình thoi

c:

Xét ΔABC có

D là trung điểm của BC

DM//AC

Do đó: M là trung điểm của AB

Để AMDN là hình vuông thì AM=AN

mà \(AM=\dfrac{AB}{2};AN=\dfrac{AC}{2}\)

nên AB=AC

a: 

\(V=\dfrac{1}{3}\cdot S\cdot h\)

=>\(S_{đáy}=V\cdot\dfrac{3}{h}=1280\cdot\dfrac{3}{15}=256\)

Độ dài cạnh đáy là: \(\sqrt{256}=16\left(cm\right)\)

b:

Chu vi đáy là:

16*4=64(cm)

Diện tích xung quanh là;

\(64\cdot17=1088\left(cm^2\right)\)

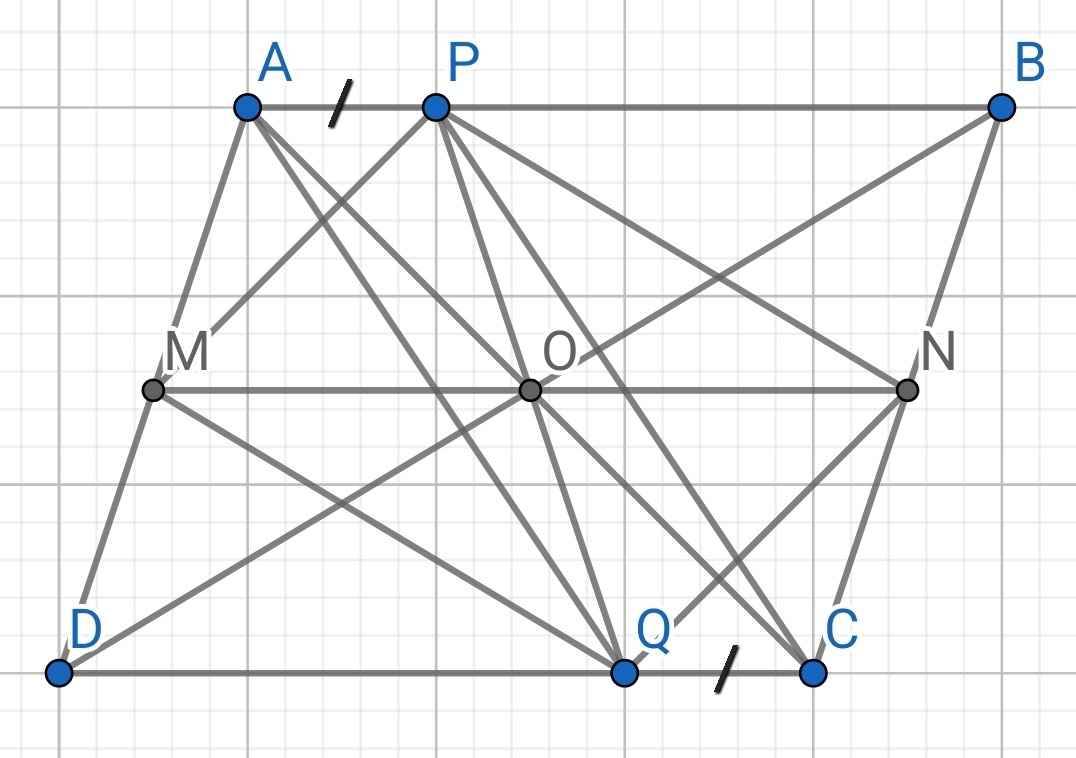   a) *) Chứng minh AMNB là hình bình hành:

Do O là giao điểm của AC và BD

Mà ABCD là hình bình hành (gt)

⇒ O là trung điểm của AC và BD

Do MN // AB (gt)

⇒ OM // CD

∆ACD có

O là trung điểm AC

OM // CD

⇒ M là trung điểm AD

⇒ AM = AD : 2   (1)

Do MN // AB (gt)

⇒ ON // AB

∆ABC có:

O là trung điểm AC (cmt)

ON // AB (cmt)

⇒ N là trung điểm BC

⇒ BN = BC : 2   (2)

Do ABCD là hình bình hành (gt)

⇒ AD // BC

⇒ AM // BN

Từ (1) và (2) ⇒ AM = BN

Tứ giác AMNB có:

AM // BN (cmt)

AM = BN (cmt)

⇒ AMNB là hình bình hành

*) Chứng minh APCQ là hình bình hành

Do ABCD là hình bình hành (gt)

⇒ AB // CD

⇒ AP // CQ

Tứ giác APCQ có:

AP // CQ (cmt)

AP = CQ (gt)

⇒ APCQ là hình bình hành

c) Do O là trung điểm AC (cmt)

M là trung điểm AD (cmt)

⇒ OM là đường trung bình của ∆ACD

⇒ OM = CD : 2   (3)

Do O là trung điểm AC (cmt)

N là trung điểm BC (cmt)

⇒ ON là đường trung bình của ∆ABC

⇒ ON = AB : 2

Mà AB = CD (do ABCD là hình bình hành)

⇒ OM = ON

⇒ O là trung điểm MN

Do APCQ là hình bình hành (cmt)

O là trung điểm AC (cmt)

⇒ O là trung điểm PQ

Tứ giác MPNQ có:

O là trung điểm MN (cmt)

O là trung điểm PQ (cmt)

⇒ MPNQ là hình bình hành

⇒ MP // NQ và MQ = NP

a) Thể tích của kim tự tháp Louvie :

\(V=\dfrac{1}{3}S_{đáy}.h=\dfrac{1}{3}.34.34.21=8092\left(m^3\right)\)

b) Diện tích 1 viên gạch vuông \(60cm\) là :

\(60.60=3600\left(cm^2\right)=0,36\left(m^2\right)\)

Số viên gạch để lót sàn kim tự tháp là :

\(1000:0,36\sim2778\left(viên\right)\)

c) Diện tích 1 mặt kim tự tháp là tam giác đều :

\(S_{\Deltađều}=\dfrac{34.34.\sqrt[]{3}}{4}=289\sqrt[]{3}\sim501\left(m^2\right)\)

Số tấm kính hình thoi 1 mặt là :

\(501:17\sim30\left(tấm\right)\)

Đáp số...

a: M là trung điểm của AB

=>\(MA=MB=\dfrac{AB}{2}\)

mà \(CD=\dfrac{AB}{2}\)

nên MA=MB=CD

Xét tứ giác AMCD có

AM//DC

AM=DC

Do đó: AMCD là hình bình hành

Xét tứ giác DCBM có

DC//BM

DC=BM

Do đó: DCBM là hình bình hành

b: DCBM là hình bình hành

=>DM//CB

=>\(\widehat{AMD}=\widehat{CBM}\)(hai góc đồng vị)

mà \(\widehat{CBM}=\widehat{ECD}\)(hai góc đồng vị, DC//AB)

nên \(\widehat{DMA}=\widehat{ECD}\)

Xét ΔEAB có DC//AB

nên \(\dfrac{ED}{EA}=\dfrac{DC}{AB}=\dfrac{1}{2}\)

=>\(ED=\dfrac{1}{2}EA\)

=>D là trung điểm của EA

=>ED=DA

Gọi K là trung điểm của HD

Xét ΔHDC có

K,M lần lượt là trung điểm của HD,HC

=>KM là đường trung bình của ΔHDC

=>KM//DC và \(KM=\dfrac{DC}{2}\)

KM//DC

AB//DC

Do đó: KM//AB

KM//DC

DC\(\perp\)AD

Do đó: \(MK\perp AD\)

Xét ΔADM có

MK,DHlà đường cao

MK cắt DH tại K

Do đó: K là trực tâm của ΔADM

=>AK\(\perp\)DM

mà BM\(\perp\)DM

nên AK//BM

Xét tứ giác ABMK có

AB//MK

AK//BM

Do đó: ABMK là hình bình hành

=>MK=AB

=>CD=2AB