Bài 4: Cho ∆ABC vuông tại A, AM là trung tuyến. I là trung điểm AC a) Chứng minh tứ giác ABMI là hình thang vuông.
b) D đối xứng M qua I. Chứng minh tứ giác ADCM là hình thoi
c) Kẻ MHL AB, IH cắt AM tại O, CO cắt IM tại K. Chứng minh: DK = 2KM
Bài 4: Cho ∆ABC vuông tại A, AM là trung tuyến. I là trung điểm AC a) Chứng minh tứ giác ABMI là hình thang vuông.
b) D đối xứng M qua I. Chứng minh tứ giác ADCM là hình thoi
c) Kẻ MHL AB, IH cắt AM tại O, CO cắt IM tại K. Chứng minh: DK = 2KM
a: Xét ΔABC có
M,I lần lượt là trung điểm của CB,CA
=>MI là đường trung bình của ΔABC
=>MI//AB và \(MI=\dfrac{AB}{2}\)
Xét tứ giác ABMI có MI//AB
nên ABMI là hình thang
Hình thang ABMI có AB\(\perp\)AI
nên ABMI là hình thang vuông
b: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
Xét tứ giác AMCD có
I là trung điểm chung của AC và MD
=>AMCD là hình bình hành
Hình bình hành AMCD có MA=MC
nên AMCD là hình thoi
c: AMCD là hình thoi
=>AC\(\perp\)MD tại I
Xét tứ giác AHMI có
\(\widehat{AHM}=\widehat{AIM}=\widehat{HAI}=90^0\)
=>AHMI là hình chữ nhật
=>AM cắt HI tại trung điểm của mỗi đường và AM=HI
=>O là trung điểm chung của AM và HI
Xét ΔCAM có
CO,MI là các đường trung tuyến
CO cắt MI tại K
Do đó: K là trọng tâm của ΔCAM
Xét ΔCAM có
MI là đường trung tuyến
K là trọng tâm của ΔCAM
Do đó: \(MK=\dfrac{2}{3}\cdot MI=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot MD=\dfrac{1}{3}MD\)
Ta có: MK+KD=MD
=>\(KD+\dfrac{1}{3}MD=MD\)
=>\(KD=\dfrac{2}{3}MD\)
=>\(KD=2\cdot\dfrac{1}{3}MD=2\cdot MI\)
Bài 5: Cho ∆ABC nhọn ( AB < AC), gọi D và E lần lượt là trung điểm của AB và AC
a) CM: tứ giác BDEC là hình thang
b) Qua D kẻ Dx song song với AC cắt BC tại F, gọi G là trung điểm của DC, CM: 3 điểm
E,G, F thẳng hàng
c) Gọi H là giao điểm của BG và DF, AH cắt GF tại I. CM: H là trọng tâm ABDC và BI //
CD
a: Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và \(DE=\dfrac{BC}{2}\)
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
b: Xét tứ giác DECF có
DE//CF
DF//CE
Do đó: DECF là hình bình hành
=>DC cắt EF tại trung điểm của mỗi đường
mà G là trung điểm của DC
nên G là trung điểm của EF
=>E,G,F thẳng hàng
c: Xét ΔABC có
D là trung điểm của BA
DF//AC
Do đó: F là trung điểm của BC
Xét ΔDBC có
DF,BG là các đường trung tuyến
DF cắt BG tại H
Do đó: H là trọng tâm của ΔDBC
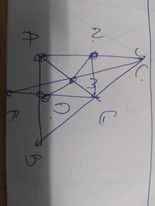
a: Xét ΔABC có
E là trung điểm của BC
D là trung điểm của BA
Do đó: ED là đường trung bình của ΔABC
=>ED//AC và \(ED=\dfrac{AC}{2}\)
Ta có: ED//AC
F\(\in\)ED
Do đó: EF//AC
Ta có: ED//AC
AB\(\perp\)AC
Do đó: ED\(\perp\)AB
=>EF\(\perp\)AB
Ta có: \(ED=\dfrac{AC}{2}\)
\(ED=\dfrac{EF}{2}\)
Do đó: AC=EF
Xét tứ giác AEBF có
D là trung điểm chung của AB và EF
=>AEBF là hình bình hành
Hình bình hành AEBF có AB\(\perp\)EF
nên AEBF là hình thoi
b: Xét tứ giác ECAF có
FE//AC
FE=AC
Do đó: ECAF là hình bình hành
c: ta có: ECAF là hình bình hành
=>EA cắt FC tại trung điểm của mỗi đường
mà M là trung điểm của EA
nên M là trung điểm của FC
=>C,M,F thẳng hàng
d: Ta có: \(DF=\dfrac{EF}{2}\)
\(CN=\dfrac{CA}{2}\)
mà EF=CA
nên DF=CN
Xét tứ giác DFNC có
DF//NC
DF=NC
Do đó: DFNC là hình bình hành
=>DN cắt FC tại trung điểm của mỗi đường
mà M là trung điểm của CF
nên M là trung điểm của DN
Xét tứ giác ADEN có
M là trung điểm chung của AE và DN
=>ADEN là hình bình hành
Hình bình hành ADEN có \(\widehat{DAN}=90^0\)
nên ADEN là hình chữ nhật
e: Khi BEAF là hình vuông thì \(\widehat{AEB}=90^0\)
=>AE\(\perp\)EB tại E
=>AE\(\perp\)BC tại E
Xét ΔABC có
AE là đường cao
AE là đường trung tuyến
Do đó: ΔABC cân tại A
Xét ΔABC cân tại A có \(\widehat{BAC}=90^0\)
nên ΔABC vuông cân tại A
=>Điều này đúng
Ta có: ΔABC cân tại A
mà AE là đường trung tuyến
nên AE là phân giác của góc BAC
Hình chữ nhật ADEN có AE là phân giác của góc DAN
nên ADEN là hình vuông
a: Xét ΔABC có
E là trung điểm của BC
D là trung điểm của BA
Do đó: ED là đường trung bình của ΔABC
=>ED//AC và \(ED=\dfrac{AC}{2}\)
Ta có: ED//AC
F\(\in\)ED
Do đó: EF//AC
Ta có: ED//AC
AB\(\perp\)AC
Do đó: ED\(\perp\)AB
=>EF\(\perp\)AB
Ta có: \(ED=\dfrac{AC}{2}\)
\(ED=\dfrac{EF}{2}\)
Do đó: AC=EF
Xét tứ giác AEBF có
D là trung điểm chung của AB và EF
=>AEBF là hình bình hành
Hình bình hành AEBF có AB\(\perp\)EF
nên AEBF là hình thoi
b: Xét tứ giác ECAF có
FE//AC
FE=AC
Do đó: ECAF là hình bình hành
c: ta có: ECAF là hình bình hành
=>EA cắt FC tại trung điểm của mỗi đường
mà M là trung điểm của EA
nên M là trung điểm của FC
=>C,M,F thẳng hàng
d: Ta có: \(DF=\dfrac{EF}{2}\)
\(CN=\dfrac{CA}{2}\)
mà EF=CA
nên DF=CN
Xét tứ giác DFNC có
DF//NC
DF=NC
Do đó: DFNC là hình bình hành
=>DN cắt FC tại trung điểm của mỗi đường
mà M là trung điểm của CF
nên M là trung điểm của DN
Xét tứ giác ADEN có
M là trung điểm chung của AE và DN
=>ADEN là hình bình hành
Hình bình hành ADEN có \(\widehat{DAN}=90^0\)
nên ADEN là hình chữ nhật
e: Khi BEAF là hình vuông thì \(\widehat{AEB}=90^0\)
=>AE\(\perp\)EB tại E
=>AE\(\perp\)BC tại E
Xét ΔABC có
AE là đường cao
AE là đường trung tuyến
Do đó: ΔABC cân tại A
Xét ΔABC cân tại A có \(\widehat{BAC}=90^0\)
nên ΔABC vuông cân tại A
=>Điều này đúng
Ta có: ΔABC cân tại A
mà AE là đường trung tuyến
nên AE là phân giác của góc BAC
Hình chữ nhật ADEN có AE là phân giác của góc DAN
nên ADEN là hình vuông
bài này vẽ hình sao v ạ
a: ABCD là hình thoi
=>AC vuông góc với BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại O và O là trung điểm chung của AC và BD
Xét tứ giác OBKC có
OB//KC
BK//OC
Do đó: OBKC là hình bình hành
Hình bình hành OBKC có \(\widehat{BOC}=90^0\)
nên OBKC là hình chữ nhật
b: OBKC là hình chữ nhật
=>OK=BC
mà BC=AB(ABCD là hình thoi)
nên OB=AB
OBKC là hình chữ nhật
=>OB//KC và OB=KC
OB=KC
OB=OD
Do đó: OD=KC
OB//KC
O\(\in\)BD
Do đó: OD//KC
Xét tứ giác ODCK có
OD//CK
OD=CK
Do đó: ODCK là hình bình hành
=>DC=OK
c: Để hình chữ nhật OBKC trở thành hình vuông thì OB=OC
mà \(OB=\dfrac{BD}{2};OC=\dfrac{AC}{2}\)
nên AC=BD
cho tam giác abc vuông tại a , đường trung tuyến am. gọi i là trung tuyến của ac trên tia đối tia im lấy điểm k sao cho ik=im
a) chứng minh amck là hình thoi
b) chứng minh akmb là hình bình hành
c) tìm điều kiện của tam giác abc để tứ giác amck là hình vuông
a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}\)
Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
nên AMCK là hình bình hành
Hình bình hành AMCK có MA=MC
nên AMCK là hình thoi
b: AMCK là hình thoi
=>AK//MC và AK=MC
AK//MC
M\(\in\)BC
Do đó: AK//MB
AK=MC
MC=MB
Do đó: AK=MB
Xét tứ giác AKMB có
AK//MB
AK=MB
Do đó: AKMB là hình bình hành
c; Để hình thoi AMCK trở thành hình vuông thì \(\widehat{KCM}=90^0\)
AMCK là hình thoi
=>CA là phân giác của \(\widehat{KCM}\)
=>\(\widehat{ACM}=\dfrac{1}{2}\cdot\widehat{KCM}=45^0\)
=>\(\widehat{ACB}=45^0\)
cho tam giác abc vuông tại a có ab<ac . gọi m là trung điểm của bc , kẻ md vuông góc với ab tại d , me vuông góc với ac tại e
a) chứng minh am = de
b) chứng minh tứ giác dmce là hình bình hành
c) gọi ah là đường cao của tam giác abc (h thuộc bc) . chứng minh tứ giác dhme là hình thang cân
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
=>AM=DE
b:
MD\(\perp\)AB
AC\(\perp\)AB
Do đó: MD//AC
ME\(\perp\)AC
AB\(\perp\)AC
Do đó: ME//AB
Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
Xét ΔBAC có
M,D lần lượt là trung điểm của BC,BA
=>MD là đường trung bình của ΔBAC
=>MD//AC và \(MD=\dfrac{AC}{2}\)
\(MD=\dfrac{AC}{2}\)
\(CE=\dfrac{AC}{2}\)
Do đó: MD=CE
MD//AC
\(E\in\)AC
Do đó: MD//CE
Xét tứ giác DMCE có
DM//CE
DM=CE
Do đó: DMCE là hình bình hành
c: Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC
=>DE//HM
ΔHAC vuông tại H
mà HE là đường trung tuyến
nên \(HE=\dfrac{AC}{2}\)
mà \(MD=\dfrac{AC}{2}\)
nên HE=MD
Xét tứ giác DHME có
ED//MH
=>DHME là hình thang
Hình thang DHME có MD=HE
nên DHME là hình thang cân
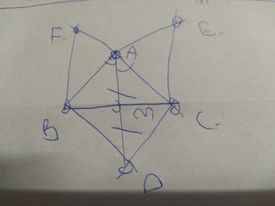
bài này vẽ hình sao v ạ

a: ΔABC cân tại A
mà AM là đường phân giác
nên AM\(\perp\)BC và M là trung điểm của BC
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: BF//AM
AM\(\perp\)BC
Do đó: BF\(\perp\)BC
=>ΔBFC vuông tại B
\(\widehat{ABC}+\widehat{ABF}=\widehat{FBC}=90^0\)
\(\widehat{ACB}+\widehat{AFB}=90^0\)(ΔBFC vuông tại B)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABF}=\widehat{AFB}\)
=>AB=AF
mà AB=AC
nên AF=AC
=>A là trung điểm của CF
AM\(\perp\)BC
EC//AM
Do đó: CE\(\perp\)CB
=>ΔCBE vuông tại C
\(\widehat{ACB}+\widehat{ACE}=\widehat{ECB}=90^0\)
\(\widehat{ABC}+\widehat{AEC}=90^0\)(ΔECB vuông tại C)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ACE}=\widehat{AEC}\)
=>AC=AE
mà AB=AC
nên AB=AE
=>A là trung điểm của BE
\(BE=2BA\)
CF=2CA
mà BA=CA
nên BE=CF
Xét tứ giác BCEF có
A là trung điểm chung của BE và CF
=>BCEF là hình bình hành
Hình bình hành BCEF có BE=CF
nên BCEF là hình chữ nhật
c: Để hình thoi ABDC là hình vuông thì \(\widehat{BAC}=90^0\)