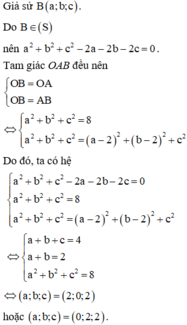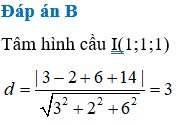Trong không gian Oxyz , cho mặt cầu (S): x2+y2+z2-2x-2y-7=0 và điểm M(2;01).Mặt phẳng (P) thay đổi đi qua M và cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng r . Khi r đạt giá trị nhỏ nhất, khoảng cách từ O đến mặt phẳng (P) bằng
H24
Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
y
-
2
z
-
1
0
và mặt phẳng
P
:
2
x
+
2
y
-
2
z
+
15...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho mặt cầu S : x 2 + y 2 + z 2 - 2 y - 2 z - 1 = 0 và mặt phẳng P : 2 x + 2 y - 2 z + 15 = 0 . Khoảng cách ngắn nhất giữa điểm (M) trên (S) và điểm N trên (P) bằng
A. 3 3 2
B. 3 2 3
C. 3 2
D. 2 3
Mặt cầu (S) có tâm I(0;1;1) và bán kính R = 3
Ta có 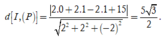
Vậy khoảng cách ngắn nhất: ![]()
Chọn A.
Đúng 0
Bình luận (0)
Trong không gian OxyzOxyz, cho mặt cầu (S):x2+y2+z2−2x−2y−7=0(S):x2+y2+z2−2x−2y−7=0 và điểm M(2;0;1)M(2;0;1). Mặt phẳng (P)(P) thay đổi đi qua MM và cắt mặt cầu (S)(S) theo giao tuyến là một đường tròn có bán kính bằng rr. Khi rr đạt giá trị nhỏ nhất, khoảng cách từ OO đến mặt phẳng (P)(P) bằng
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x+2y-2z+150 và mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
y
-
2
z
-
1
0
Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu (S) là A. ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x+2y-2z+15=0 và mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 y - 2 z - 1 = 0 Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu (S) là
A. 3 3 2
B. 3
C. 3 2
D. 3 3
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
+
4
x
-
6
y
+
m
0
và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P):
2
x
-
2
y
-
z
+
1
0
, (Q):
x
+
2
y
-
2
z
-
4
0
....
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 + 4 x - 6 y + m = 0 và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P): 2 x - 2 y - z + 1 = 0 , (Q): x + 2 y - 2 z - 4 = 0 . Tìm m để (S) cắt (d) tại 2 điểm M, N sao cho độ dài MN = 8.
A. m = 2
B. m = -12
C. m = 12
D. m = -2
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
+
4
x
-
6
y
+
m
0
và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P):
2
x
-
2
y
-
z
+
1
0
, (Q):
x
+
2
y
-
2
z
-
4
0
....
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 + 4 x - 6 y + m = 0 và đường thẳng (d) là giao tuyến của 2 mặt phẳng (P): 2 x - 2 y - z + 1 = 0 , (Q): x + 2 y - 2 z - 4 = 0 . Tìm m để (S) cắt (d) tại 2 điểm M, N sao cho độ dài MN = 8.
A. m = 2
B. m = -12
C. m = 12
D. m = -2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
2
y
-
2
z
0
và điểm
A
2
;
2
;
0
. Viết phương...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 2 x - 2 y - 2 z = 0 và điểm A 2 ; 2 ; 0 . Viết phương trình mặt phẳng O A B , biết rằng điểm B thuộc mặt cầu S , có hoành độ dương và tam giác OAB đều.
A. x - y + 2 z = 0
B. x - y - 2 z = 0
C. x - y - z = 0
D. x - y + z = 0
Trong không gian Oxyz, cho điểm
A
(
-
3
2
;
0
;
0
)
và mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
-
3
0
. M là điểm bất kỳ trên mặt cầu (S), khoảng cách AM nhỏ nhất là: A. ...
Đọc tiếp
Trong không gian Oxyz, cho điểm A ( - 3 2 ; 0 ; 0 ) và mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 3 = 0 . M là điểm bất kỳ trên mặt cầu (S), khoảng cách AM nhỏ nhất là:
A. 5 2
B. 1 4
C. 3 2
D. 1 2
Trong không gian Oxyz cho điểm
A
-
3
2
;
0
;
0
và mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
3
0
. M là điểm...
Đọc tiếp
Trong không gian Oxyz cho điểm A - 3 2 ; 0 ; 0 và mặt cầu S : x 2 + y 2 + z 2 - 2 x - 3 = 0 . M là điểm bất kỳ trên mặt cầu (S), khoảng cách AM nhỏ nhất là:
A. 5 2
B. 1 4
C. 3 2
D. 1 2
Đáp án D.
Mặt cầu (S) có tâm I(1;0;0) và bán kính R=2
Ta có:
![]()
Do đó khoảng cách AM nhỏ nhất là:
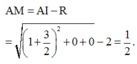
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
-
2
y
-
2
z
-
22
0
và mặt phẳng (P): 3x-2y+5z+10. Tính khoảng cách h từ tâm của (S) tới (P) A. h4 B. h3 C. h2 D. h1
Đọc tiếp
Trong không gian Oxyz cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 2 y - 2 z - 22 = 0 và mặt phẳng (P): 3x-2y+5z+1=0. Tính khoảng cách h từ tâm của (S) tới (P)
A. h=4
B. h=3
C. h=2
D. h=1
Trong không gian Oxyz, cho mặt phẳng (P): 2x - 2y + z + 1 0 và mặt cầu (S):
x
2
+
y
2
+
z
2
+ 2x + 4y - 6z + 10 0. Khẳng định nào dưới đây là đúng? A. (P) và (S) có vô số điểm chung B. (P) tiếp xúc với (S) C. (P) không cắt (S) D. Cả ba khẳng định trên đều sai
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P): 2x - 2y + z + 1 = 0 và mặt cầu (S): x 2 + y 2 + z 2 + 2x + 4y - 6z + 10 = 0. Khẳng định nào dưới đây là đúng?
A. (P) và (S) có vô số điểm chung
B. (P) tiếp xúc với (S)
C. (P) không cắt (S)
D. Cả ba khẳng định trên đều sai