\(\text{|}\dfrac{7}{5}x+\dfrac{2}{3}\text{|}\text{=}\text{|}\dfrac{4}{3}x-\dfrac{1}{4}\text{|}\)
HH
Những câu hỏi liên quan
1.Tính a,5text{x}dfrac{7}{3} b,dfrac{13}{4}:72.Tính a,dfrac{3}{7}+dfrac{2}{5}+dfrac{3}{4} b,dfrac{9}{7}-dfrac{5}{11}text{x}dfrac{11}{7} c,dfrac{3}{5}text{x}dfrac{5}{7}text{+}dfrac{4}{7} d,dfrac{7}{9}text{x}dfrac{2}{5}:dfrac{3}{11} e,dfrac{9}{7}+dfrac{2}{3}-dfrac{1}{4} g,dfrac{4}{9}:dfrac{3}{5}text{x}dfrac{2}{11} h,dfrac{7}{2}-dfrac{3}{10}:dfrac{2}{5}
Đọc tiếp
1.Tính
\(a,5\text{x}\dfrac{7}{3}\) \(b,\dfrac{13}{4}:7\)
2.Tính
\(a,\dfrac{3}{7}+\dfrac{2}{5}+\dfrac{3}{4}\) \(b,\dfrac{9}{7}-\dfrac{5}{11}\text{x}\dfrac{11}{7}\) \(c,\dfrac{3}{5}\text{x}\dfrac{5}{7}\text{+}\dfrac{4}{7}\) \(d,\dfrac{7}{9}\text{x}\dfrac{2}{5}:\dfrac{3}{11}\) e,\(\dfrac{9}{7}+\dfrac{2}{3}-\dfrac{1}{4}\)
g,\(\dfrac{4}{9}:\dfrac{3}{5}\text{x}\dfrac{2}{11}\) h,\(\dfrac{7}{2}-\dfrac{3}{10}:\dfrac{2}{5}\)
\(a,5x\dfrac{7}{3}=\dfrac{5}{1}x\dfrac{7}{3}=\dfrac{35}{3};b,\dfrac{13}{4}:7=\dfrac{13}{4} :\dfrac{7}{1}=\dfrac{13}{4}x\dfrac{1}{7}=\dfrac{13}{28}\)
Đúng 0
Bình luận (0)
\(\dfrac{3}{7}+\dfrac{2}{5}+\dfrac{3}{4}=\dfrac{60}{140}+\dfrac{56}{140}+\dfrac{105}{140}=\dfrac{221}{140}\)
Đúng 0
Bình luận (0)
\(\dfrac{9}{7}-\dfrac{5}{11}x\dfrac{11}{7}=\dfrac{9}{7}-\dfrac{5}{7}=\dfrac{4}{7}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
dfrac{-7}{x}text{}dfrac{-21}{x-34} dfrac{4-x}{-5}text{}dfrac{-5}{4-x} dfrac{3}{x+2}text{}dfrac{5}{2x+1} dfrac{1}{2}text{}dfrac{x+1}{3x} dfrac{-3}{x+1}text{}dfrac{4}{2-2x}
Đọc tiếp
\(\dfrac{-7}{x}\text{=}\dfrac{-21}{x-34}\) \(\dfrac{4-x}{-5}\text{=}\dfrac{-5}{4-x}\)
\(\dfrac{3}{x+2}\text{=}\dfrac{5}{2x+1}\) \(\dfrac{1}{2}\text{=}\dfrac{x+1}{3x}\)
\(\dfrac{-3}{x+1}\text{=}\dfrac{4}{2-2x}\)
\(\dfrac{4-x}{-5}=\dfrac{-5}{4-x}\)
\(\left(4-x\right)^2=25=5^2=\left(-5\right)^2\)
4-x=5 hoặc 4-x=-5
x=-1 hoặc x=9
Đúng 0
Bình luận (1)
a,\(\dfrac{1}{7}\text{x}\dfrac{2}{7}+\dfrac{1}{7}\text{x}\dfrac{5}{7}+\dfrac{6}{7}\) b,\(\dfrac{6}{11}\text{x}\dfrac{4}{9}+\dfrac{6}{11}\text{x}\dfrac{7}{9}-\dfrac{6}{11}\text{x}\dfrac{2}{9}\)
c, \(\dfrac{4}{25}\text{x}\dfrac{5}{8}\text{x}\dfrac{25}{4}\text{x}24\)
`a)1/7xx2/7+1/7xx5/7+6/7`
`=1/7xx(2/7+5/7)+6/7`
`=1/7xx1+6/7`
`=1/7+6/7=1`
`b)6/11xx4/9+6/11xx7/9-6/11xx2/9`
`=6/11xx(4/9+7/9-2/9)`
`=6/11xx9/9`
`=6/11`
Đúng 3
Bình luận (0)
Sorry nãy ghi thiếu.
`c)4/25xx5/8xx25/4xx24`
`=(4xx5xx25xx24)/(25xx8xx4)`
`=(4xx5xx24)/(4xx8)`
`=(5xx24)/8`
`=5xx3=15`
Đúng 3
Bình luận (0)
a, \(\dfrac{1}{7}.\dfrac{2}{7}+\dfrac{1}{7}.\dfrac{5}{7}+\dfrac{6}{7}\)
\(=\dfrac{1}{7}.\left(\dfrac{2}{7}+\dfrac{5}{7}\right)+\dfrac{6}{7}\)
\(=\dfrac{1}{7}.1+\dfrac{6}{7}\)
\(=\dfrac{1}{7}+\dfrac{6}{7}=1\)
b, \(\dfrac{6}{11}.\dfrac{4}{9}+\dfrac{6}{11}.\dfrac{7}{9}-\dfrac{6}{11}.\dfrac{2}{9}\)
\(=\dfrac{6}{11}.\left(\dfrac{4}{9}+\dfrac{7}{9}-\dfrac{2}{9}\right)\)
\(=\dfrac{6}{11}.1=\dfrac{6}{11}\)
c, \(\dfrac{4}{25}.\dfrac{5}{8}.\dfrac{25}{4}.24\)
\(=\left(\dfrac{4}{25}.\dfrac{25}{4}\right).\left(\dfrac{5}{8}.24\right)\)
\(=1.15=15\)
Đúng 2
Bình luận (1)
Cho x + 3y - 2z = 36. Tìm x,y,z biết
a) \(\dfrac{\text{x-1}}{\text{3}}=\dfrac{\text{y+2}}{\text{4}}=\dfrac{\text{z-2}}{\text{3}}\)
b) \(\dfrac{\text{x}}{\text{4}}=\dfrac{\text{y}}{\text{3}};\dfrac{\text{y}}{\text{2}}=\dfrac{\text{z}}{\text{5}}\)
c) 9x = 5y ; 2x = z
d) 2x = 3y = 4z
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x+3y-2z}{\dfrac{1}{2}+3\cdot\dfrac{1}{3}-2\cdot\dfrac{1}{4}}=\dfrac{36}{1}=36\)
Do đó: x=18; y=12; z=9
Đúng 0
Bình luận (0)
\(\text{|}\dfrac{5}{4}x-\dfrac{7}{2}\text{|}-\text{|}\dfrac{5}{8}x+\dfrac{3}{5}\text{|}\text{=}0\)
`|5/4 x-7/2| -|5/8 x +3/5|=0`
`|5/4 x-7/2|=|5/8 x+3/5|`
\(\left[{}\begin{matrix}\dfrac{5}{4}x-\dfrac{7}{2}=\dfrac{5}{8}x+\dfrac{3}{5}\\\dfrac{5}{4}x-\dfrac{7}{2}=-\dfrac{5}{8}x-\dfrac{3}{5}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{164}{25}\\x=\dfrac{116}{75}\end{matrix}\right.\)
Vậy....
Đúng 4
Bình luận (1)
\(\left|\dfrac{5}{4}x-\dfrac{7}{2}\right|-\left|\dfrac{5}{8}x+\dfrac{3}{5}\right|=0\)
\(\Rightarrow\left|\dfrac{5}{4}x-\dfrac{7}{2}\right|=\left|\dfrac{5}{8}x+\dfrac{3}{5}\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{5}{4}x-\dfrac{7}{2}=\dfrac{5}{8}x+\dfrac{3}{5}\\\dfrac{5}{4}x-\dfrac{7}{2}=-\dfrac{5}{8}x-\dfrac{3}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{164}{25}\\x=\dfrac{116}{75}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho x + 3y - 2z = 36 . Tìm x,y,z biết :
a)\(\dfrac{\text{x-1}}{\text{3}}=\dfrac{\text{y+2}}{\text{4}}=\dfrac{\text{z-2}}{\text{3}}\)
b)\(\dfrac{\text{x}}{\text{4}}=\dfrac{\text{y}}{3};\dfrac{\text{y}}{\text{2}}=\dfrac{\text{z}}{\text{5}}\)
c) 9x = 5y ; 2x = z
d) 2x = 3y = 4z
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{x+3y-2z}{\dfrac{1}{2}+3\cdot\dfrac{1}{3}-2\cdot\dfrac{1}{4}}=\dfrac{36}{1}=36\)
Do đó: x=18; y=12; z=9
Đúng 0
Bình luận (0)
a) Thay x + 3y - 2z vào biểu thức ta có:
\(\dfrac{x - 1}{3} = \dfrac{3(y + 2)}{3 . 4} = \dfrac{2(z - 2)}{2 . 3}\) = \(\dfrac{x - 1}{3} = \dfrac{3x + 6}{12} = \dfrac{2z - 4}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhua ta có:
\(\dfrac{x - 1}{3} = \dfrac{3y + 6}{12} = \dfrac{2z - 4}{6} = \dfrac{x - 1}{3}+ \dfrac{3y + 6}{12} -\dfrac{2z - 4}{6}\)
=\(\dfrac{x - 1 + 3y + 6 - 2z + 4}{3 + 12 -6} \) = \(\dfrac{(x + 3y - 2z) + ( -1 + 6 +4)}{3 + 12 - 6} \)
=\(\dfrac{36 + 9}{9}\) = 5
=> \(\dfrac{x - 1}{3} =\) 5 => x - 1 = 5.3 =15 => x = 5+1 = 6
=>
=>
Vậy ...
(Bạn dựa theo cách này và lm những bài tiếp nhé!)
Đúng 0
Bình luận (0)
rút gọn các biểu thức sau
\(B=\dfrac{3\text{x}^2+6\text{x}+12}{x^3-8\dfrac{ }{ }}\)
C=\(\left(\dfrac{x+1}{2\text{x}-2}+\dfrac{3}{x^2-1}-\dfrac{x+3}{2\text{x}+2}\right).\dfrac{4\text{x}^2-4}{5}\)
E=\(\dfrac{x^2-10\text{x}+25}{x^2-5\text{x}}\)
mình cần gấp mong các bạn giải giùm
Đúng 0
Bình luận (0)
c: \(E=\dfrac{\left(x-5\right)^2}{x\left(x-5\right)}=\dfrac{x-5}{x}\)
Đúng 1
Bình luận (0)
Tìm số thập phân x biết:a) ^{text{x}}^{ }+ dfrac{3}{4} dfrac{4}{5}b) ^{text{x}} - dfrac{1}{2} dfrac{5}{8}c) ^{text{x}} x dfrac{5}{6} dfrac{4}{5} d)^{text{x}} : dfrac{5}{8} dfrac{1}{25}
Đọc tiếp
Tìm số thập phân x biết:
a) \(^{\text{x}}\)\(^{ }\)+ \(\dfrac{3}{4}\)= \(\dfrac{4}{5}\) | b) \(^{\text{x}}\) - \(\dfrac{1}{2}\) = \(\dfrac{5}{8}\) | c) \(^{\text{x}}\) x \(\dfrac{5}{6}\) = \(\dfrac{4}{5}\) | d)\(^{\text{x}}\) : \(\dfrac{5}{8}\) = \(\dfrac{1}{25}\) |
a) \(x=0,05\)
b) \(x=1,125\)
c) \(x=0,96\)
d) \(x=0,025\)
Đúng 1
Bình luận (0)
Bạn tự làm đi dễ mà . Cố mag vận động đầu óc đừng copy làm bài nữa khó lắm mới hỏi thôi
Đúng 1
Bình luận (0)
Giải các bất phương trình sau
1) \(\dfrac{\text{x - 2}}{x+1}-\dfrac{3}{x+2}>0\) 2) \(\dfrac{\text{x + 1}}{x+2}+\dfrac{x}{x-3}\le0\)
3) \(\dfrac{\text{x}^2+2x+5}{x+4}>x-3\) 4) \(\sqrt{\text{x^2}-3x+2}\ge3\)
\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
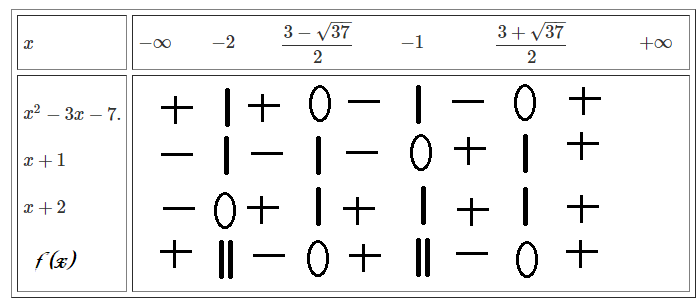
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
Đúng 1
Bình luận (0)







