Viết những hằng đẳng thức đáng nhớ GIÚP MK NHA (VIẾT HẾT RA NHA )
KL
Những câu hỏi liên quan
có bao nhiêu hằng đẳng thức đáng nhớ???
nhanh mk tik
kb vs mk nha
có 7 hằng đẳng thức đáng nhớ ( quan trọng ) được học ở lớp 8
ngoài ra còn khà nhiều
Đúng 0
Bình luận (0)
1. Bình phương của một tổng 2. Bình phương của một hiệu
2. Bình phương của một hiệu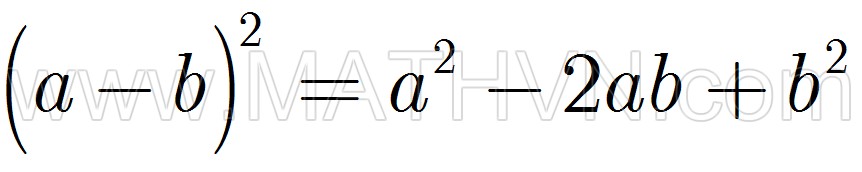 3. Hiệu của hai bình phương
3. Hiệu của hai bình phương 4. Lập phương của một tổng
4. Lập phương của một tổng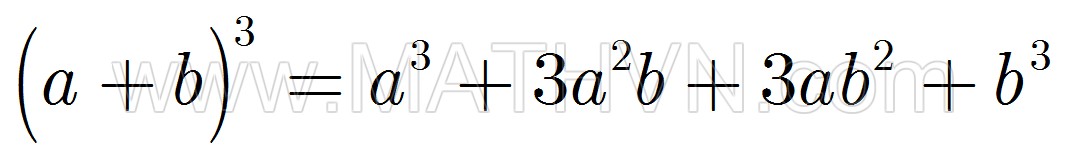 5. Lập phương của một hiệu
5. Lập phương của một hiệu 6. Tổng của hai lập phương
6. Tổng của hai lập phương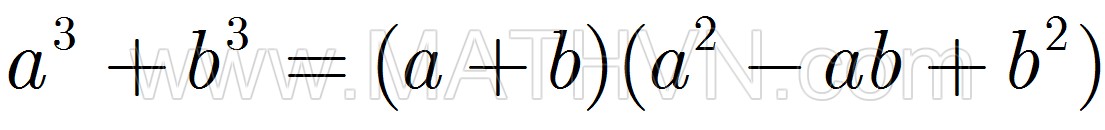 7. Hiệu của hai lập phương
7. Hiệu của hai lập phương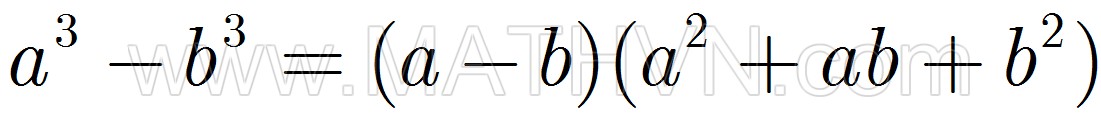 8. Tổng hai bình phương
8. Tổng hai bình phương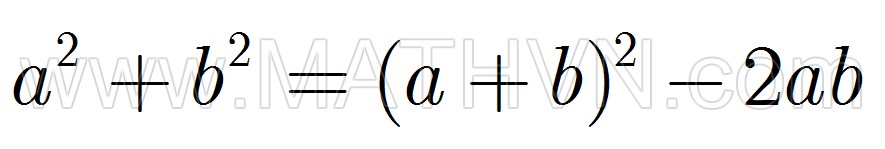 9. Tổng hai lập phương
9. Tổng hai lập phương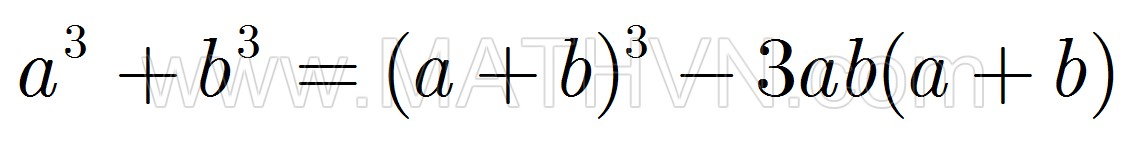 10. Bình phương của tổng 3 số hạng
10. Bình phương của tổng 3 số hạng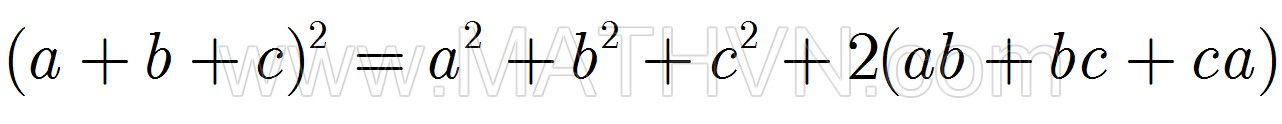 11. Lập phương của tổng 3 số hạng
11. Lập phương của tổng 3 số hạng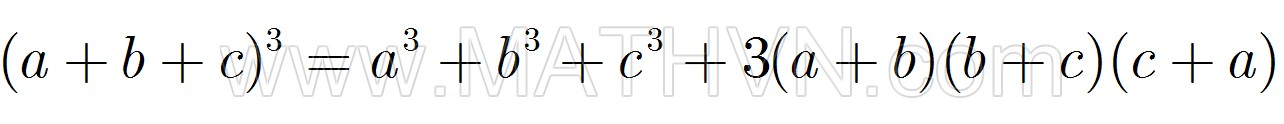
 2. Bình phương của một hiệu
2. Bình phương của một hiệu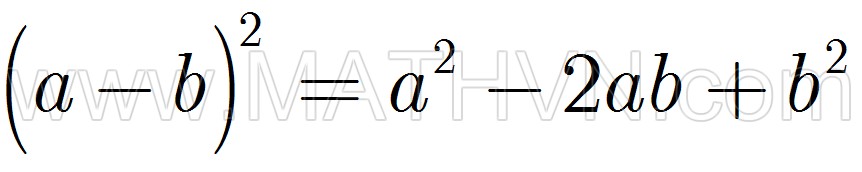 3. Hiệu của hai bình phương
3. Hiệu của hai bình phương 4. Lập phương của một tổng
4. Lập phương của một tổng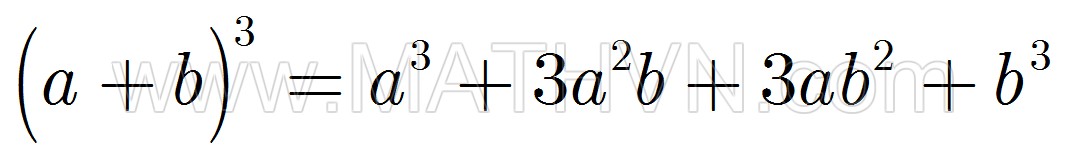 5. Lập phương của một hiệu
5. Lập phương của một hiệu 6. Tổng của hai lập phương
6. Tổng của hai lập phương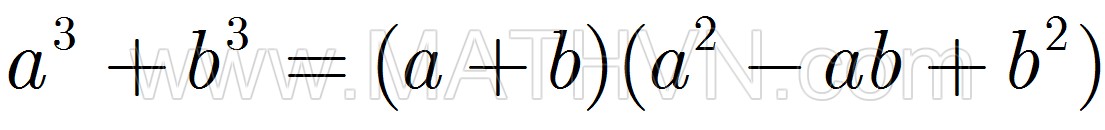 7. Hiệu của hai lập phương
7. Hiệu của hai lập phương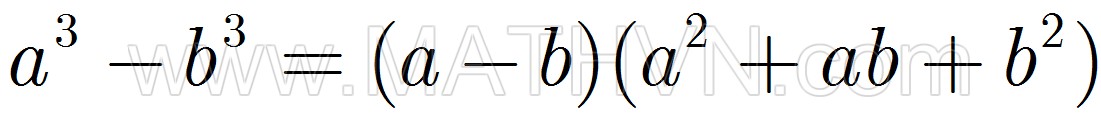 8. Tổng hai bình phương
8. Tổng hai bình phương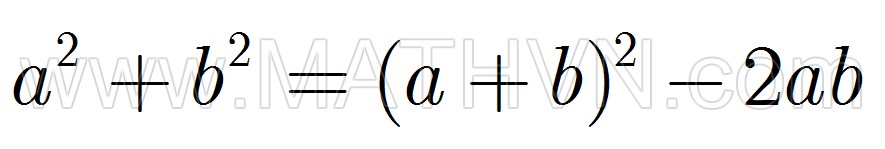 9. Tổng hai lập phương
9. Tổng hai lập phương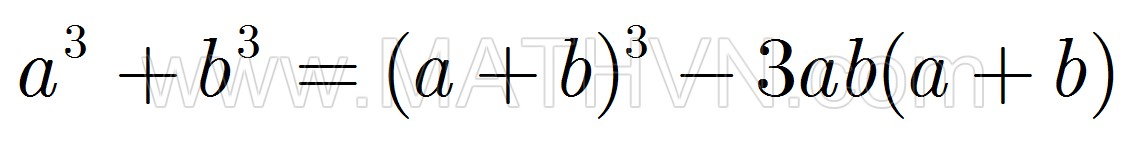 10. Bình phương của tổng 3 số hạng
10. Bình phương của tổng 3 số hạng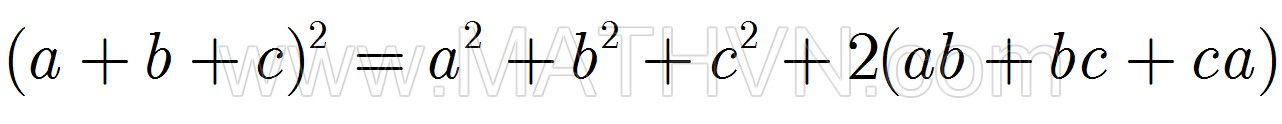 11. Lập phương của tổng 3 số hạng
11. Lập phương của tổng 3 số hạng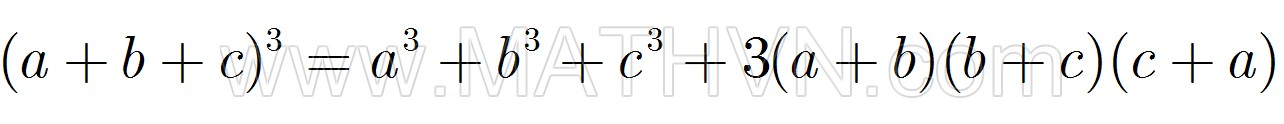
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Trả lời hộ mình + làm đúng = Mình Tích cho nha !
Bài 1:Viết biểu thức sau thành bình phương của 1 tổng(hiệu):
x^2y^2 + 4xy + 4 ( Gợi ý: Hãy dùng những hằng đẳng thức đáng nhớ ).
nó dễ ợt mà -_-
x2y2+4xy+4=(xy+2)2 xong :))
Đúng 0
Bình luận (0)
Viết bảy hằng đẳng thức đáng nhớ.
Bảy hằng đẳng thức đáng nhớ:
1) (A + B)2 = A2 + 2AB + B2
2) (A – B)2 = A2 – 2AB + B2
3) A2 – B2 = (A – B)(A + B)
4) (A + B)3 = A3 + 3A2B + 3AB2 + B3
5) (A – B)3 = A3 – 3A2B + 3AB2 – B3
6) A3 + B3 = (A + B)(A2 – AB + B2)
7) A3 – B3 = (A – B)(A2 + AB + B2)
Đúng 0
Bình luận (0)
Viết 5 hằng đẳng thức đáng nhớ
\(\left(a+b\right)^2=a^2+2ab+b^2\)
\(\left(a-b\right)^2=a^2-2ab+b^2\)
\(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
\(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
\(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)
Đúng 1
Bình luận (1)
\(\left(a+b\right)^2=a^2+ab+b^2\)
\(\left(a-b\right)^2=a^2-2ab+b^2\)
\(a^2-b^2=\left(a+b\right)\left(a-b\right)\)
\(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\)
Đúng 1
Bình luận (2)
Xem thêm câu trả lời
27a3-8 lm giúp mik vs
lm những hằng thức đáng nhớ nha
Viết bẩy hằng đẳng thức đáng nhớ ?
Ta có bảy hằng đẳng thức đáng nhớ:
1. (A + B)2 = A2 + 2AB + B2
2. (A – B)2 = A2 – 2AB + B2
3. A2 – B2 = (A + B)(A – B)
4. (A + B)3 = A3 + 3A2B + 3AB2 + B3
5. (A – B)3 = A3 – 3A2B + 3AB2 – B3
6. A3 + B3 = (A + B)(A2 – AB + B2)
7. A3 – B3 = (A – B)(A2 + AB + B2)
Đúng 0
Bình luận (0)
\(\left(A-B\right)^2=A^2-2AB-B^2\)
\(\left(A+B\right)^2=A^2+2AB+B^2\)
\(A^2-B^2=\left(A+B\right)\left(A-B\right)\)
\(\left(A+B\right)^3=A^3+3A^2B+3AB^2+B^3\)
\(\left(A-B\right)^3=A^3-3A^2B+3AB^2-B^3\)
\(A^3+B^3=\left(A+B\right)\left(A^2-AB+B^2\right)\)
\(A^3-B^3=\left(A-B\right)\left(A^2+AB+B^2\right)\)
Đúng 0
Bình luận (0)
hãy viết bảy hằng đẳng thức đáng nhớ?
Bình phương của một tổng:
Đúng 0
Bình luận (0)
Bình phương của một tổng:
{\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}\,}
{\displaystyle (a-b)^{2}=a^{2}-2ab+b^{2}\,}
{\displaystyle a^{2}-b^{2}=(a-b)(a+b)\,}
{\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\,}
{\displaystyle (a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}\,}
{\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})=(a+b)^{3}-3a^{2}b-3ab^{2}=(a+b)^{3}-3ab(a+b)}
{\displaystyle a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})=(a-b)^{3}+3a^{2}b-3ab^{2}=(a-b)^{3}+3ab(a-b)}
Đúng 0
Bình luận (0)
Bình phương của một tổng:
{\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}\,}
{\displaystyle (a-b)^{2}=a^{2}-2ab+b^{2}\,}
{\displaystyle a^{2}-b^{2}=(a-b)(a+b)\,}
{\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\,}
{\displaystyle (a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}\,}
{\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})=(a+b)^{3}-3a^{2}b-3ab^{2}=(a+b)^{3}-3ab(a+b)}

Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Viết 7 hằng đẳng thức đáng nhớ? cho vd
vào chửi nó giúp mình với : https://olm.vn/thanhvien/thiend2k4
CHUYÊN ĐỀ: NHỮNG HẰNG ĐẲNG THỨC ĐÁNG NHỚ
A. Lý thuyết1. Bình phương của một tổng- Bình phương của một tổng bằng bình phương số thứ nhất cộng với hai lần tích số thứ nhân nhân số thứ hai rồi cộng với bình phương số thứ hai. (A + B)2 = A2 + 2AB + B2 |
Ví dụ:
2. Bình phương của một hiệu- Bình phường của một hiệu bằng bình phương số thứ nhất trừ đi hai lần tích số thứ nhất nhân số thứ 2 rồi cộng với bình phương số thứ hai. (A - B)2 = A2 - 2AB + B2 |
Ví dụ:
3. Hiệu hai bình phương- Hiệu hai bình phương bằng hiệu hai số đó nhân tổng hai số đó. A2 – B2 = (A + B)(A – B) |
Ví dụ:
4. Lập phương của một tổng- Lập phương của một tổng = lập phương số thứ nhất + 3 lần tích bình phương số thứ nhất nhân số thứ hai + 3 lần tích số thứ nhất nhân bình phương số thứ hai + lập phương số thứ hai. (A + B)3 = A3 + 3A2B + 3AB2 + B3 |
Vú dụ:
5. Lập phương của một hiệu- Lập phương của một hiệu = lập phương số thứ nhất - 3 lần tích bình phương số thứ nhất nhân số thứ hai + 3 lần tích số thứ nhất nhân bình phương số thứ hai - lập phương số thứ hai. (A - B)3 = A3 - 3A2B + 3AB2 - B3 |
Ví dụ:
6. Tổng hai lập phương- Tổng của hai lập phương bằng tổng hai số đó nhân với bình phương thiếu của hiệu. A3 + B3 = (A + B)(A2 – AB + B2) |
Ví dụ:
7. Hiệu hai lập phương- Hiệu của hai lập phương bằng hiệu của hai số đó nhân với bình phương thiếu của tổng. A3 – B3 = (A – B)(A2 + AB + B2) |
Phần bài tập ở đây nhé ( Tham khảo )
https://toanh7.com/ly-t huyet-va-bai-tap-ve-7-hang-dang-thuc-dang-nho-a10901.html
trong 7 hằng đẳng thức đáng nhớ cơ bản . các bạn có bài nào không
giúp mik tí nha các bạn
Những hằng đẳng thức đáng nhớ là lớp 8 mà bạn
Đúng 0
Bình luận (0)
Bình phương của một tổng:

Đúng 0
Bình luận (0)
https://vi.wikipedia.org/wiki/B%E1%BA%A3y_h%E1%BA%B1ng_%C4%91%E1%BA%B3ng_th%E1%BB%A9c_%C4%91%C3%A1ng_nh%E1%BB%9B
Đúng 0
Bình luận (0)












