Định lý này được đặt tên theo nhà vật lí học và nhà toán học Hy Lạp Pytago 

la py ta go

Py-ta-go chứ ai.

Ko hiêu lun đó

Thui đi

Định lý Pytago đã được biết đến từ lâu trước thời của Pythagoras, nhưng ông được coi là người đầu tiên nêu ra chứng minh định lý này.^[2] Cách chứng minh của ông rất đơn giản, chỉ bằng cách sắp xếp lại hình vẽ.

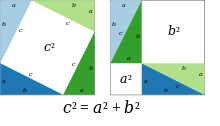
Trong hai hình vuông lớn ở hình minh họa bên trái, mỗi hình vuông chứa bốn tam giác vuông bằng nhau, sự khác nhau giữa hai hình vuông này là các tam giác vuông được bố trí khác nhau. Do vậy, khoảng trắng bên trong mỗi hình vuông phải có diện tích bằng nhau. Dựa vào hình vẽ, hai vùng trắng có diện tích bằng nhau cho phép rút ra được kết luận của định lý Pytago, Q.E.D.^[9]

Về sau, trong tác phẩm của nhà triết học và toán học Hy Lạp Proclus đã dẫn lại chứng minh rất đơn giản của Pythagoras.^[10] Các đoạn dưới đây nêu ra một vài cách chứng minh khác, nhưng cách chứng minh ở trên thuộc về của Pythagoras

theo định lý pytaogo thì : tổng bình phương 2 cạnh góc vuông = bình phương cạnh huyền nên bình phương cạnh huyền lớn hơn bình phương 2 cạnh góc vuông (ko phải tổng nhé)=> cạnh huyền là cạnh lớn nhất trong tam giác vuông .

 Tk mình nha , chúc bạn học tốt

ban co the ve hinh duoc ko hoac cho biet do la hinh j

Hình tam giác 

What, bạn đùa à, có vụ đó nữa sao. AD;AE;DE;DC chẳng có thông tin gì cả thì làm bằng niềm tin ấy

- Định lí Py – ta – go thuận:

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

- Định lí Py – ta – go đảo:

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

- Định lí Py – ta – go thuận:

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

- Định lí Py – ta – go đảo:

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

bình phương cạnh huyền = tổng bình phương. Mình nhớ py- ta-go làm gì có dạy ở Tiểu học nhỉ

dạy ở trường  cấp hai lớp 7

Trong 1 tam giac1 vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông

( định lí Py - ta - go thuận )

đây là ngử văn????? Khó wa trời

khó ghê