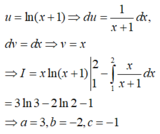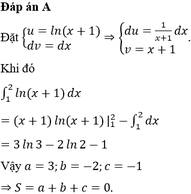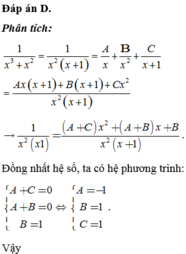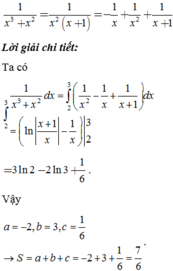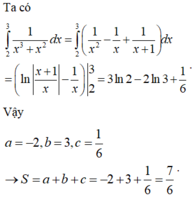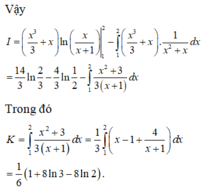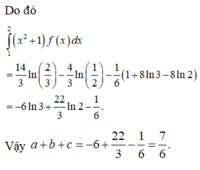Biết \(I = \int_{2}^{3}\dfrac{dx}{x^2+x} \) = aln3 + bln2, với ( a, b ϵ Z ). Tính tổng S = a + b
AH
Những câu hỏi liên quan
Biết rằng
∫
1
2
ln
(
x
+
1
)
d
x
a
ln
3
+
b
ln
2
+
c
với a,b,c là các số nguyên. Tính
S
a
+
b
+
c
. A. S1 B. S0 C. S2 D. S-2
Đọc tiếp
Biết rằng ∫ 1 2 ln ( x + 1 ) d x = a ln 3 + b ln 2 + c với a,b,c là các số nguyên. Tính S = a + b + c .
A. S=1
B. S=0
C. S=2
D. S=-2
Chọn B
Đặt u = ln ( x + 1 ) d v = d x
⇒ d u = 1 x + 1 d x v = x + 1
Khi đó
∫ 1 2 ln ( x + 1 ) d x = ( x + 1 ) ln ( x + 1 ) 1 2 - ∫ 1 2 d x = 3 ln 3 - 2 ln 2 - 1
Vậy a=3; b=-2; c=-1 ⇒ S = a + b + c = 0
Đúng 0
Bình luận (0)
Biết rằng
∫
1
2
ln
(
x
+
1
)
d
x
a
ln
3
+
b
ln
2
+
c
với a, b, c là các số nguyên. Tính S a+b+c A. S 0 B. S 1 C. S 2 D. S -2
Đọc tiếp
Biết rằng ∫ 1 2 ln ( x + 1 ) d x = a ln 3 + b ln 2 + c với a, b, c là các số nguyên. Tính S = a+b+c
A. S = 0
B. S = 1
C. S = 2
D. S = -2
Biết rằng
∫
1
2
ln
(
x
+
1
)
d
x
a
ln
3
+
b
ln
2
+
c
với a, b, c là các số nguyên. Tính S a +b + c. A. S 1 B. S 0 C. S 2 D. S -2
Đọc tiếp
Biết rằng ∫ 1 2 ln ( x + 1 ) d x = a ln 3 + b ln 2 + c với a, b, c là các số nguyên. Tính S = a +b + c.
A. S = 1
B. S = 0
C. S = 2
D. S = -2
Cho
∫
1
e
[
1
x
+
ln
x
x
(
ln
x
+
2
)
2
]
d...
Đọc tiếp
Cho ∫ 1 e [ 1 x + ln x x ( ln x + 2 ) 2 ] d x = a ln 3 + b ln 2 + c 3 với a , b , c ∈ Z . Giá trị của a 2 + b 2 + c 2 bằng
![]()
![]()
![]()
![]()
\(\int\limits^1_0xln\left(2+x^2\right)dx=aln3+bln2+c\) tính a+b+c
Đặt \(\left\{{}\begin{matrix}u=ln\left(2+x^2\right)\\dv=xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{2x}{x^2+2}dx\\v=\frac{x^2}{2}\end{matrix}\right.\)
\(\Rightarrow I=\frac{x^2}{2}.ln\left(2+x^2\right)|^1_0-\int\limits^1_0\frac{x^3}{x^2+2}dx=\frac{1}{2}ln3-I_1\)
\(I_1=\int\limits^1_0\frac{x^3}{x^2+2}dx=\int\limits^1_0\left(x-\frac{2x}{x^2+2}\right)dx=\left(\frac{x^2}{2}-ln\left(x^2+2\right)\right)|^1_0=\frac{1}{2}-ln3+ln2\)
\(\Rightarrow I=\frac{3}{2}ln3-ln2-\frac{1}{2}\)\(\Rightarrow a+b+c=\frac{3}{2}-1-\frac{1}{2}=0\)
Đúng 0
Bình luận (0)
Cho tích phân
∫
2
3
1
x
3
+
x
2
d
x
a
ln
3
+
b
ln
2
với
a
,
b
,
c
∈
ℚ
. Tính tổng
S
a
+
b
+
c
A.
S
-
2...
Đọc tiếp
Cho tích phân ∫ 2 3 1 x 3 + x 2 d x = a ln 3 + b ln 2 với a , b , c ∈ ℚ . Tính tổng S = a + b + c
A. S = - 2 3
B. S = - 7 6
C. S = 2 3
D. S = 7 6
Đáp án D.
Phân tích: 1 x 3 + x 2 = 1 x 2 x + 1 = A x + B x 2 + C x + 1 = A x ( x + 1 ) + B ( x + 1 ) + C x 2 x 2 ( x + 1 )
→ 1 x 2 ( x 1 ) = A + C x 2 + A + B x + B x 2 x + 1 .
Đồng nhất hệ số, ta có hệ phương trình:
A + C = 0 A + B = 0 B = 1 ⇔ A = - 1 B = 1 C = 1 . Vậy 1 x 3 + x 2 = 1 x 2 ( x + 1 ) = - 1 x + 1 x 2 + 1 x + 1
Lời giải chi tiết:
Ta có ∫ 2 3 1 x 3 + x 2 d x = ∫ 2 3 1 x 2 - 1 x + 1 x + 1 d x = ln x + 1 x - 1 x 2 3 = 3 ln 2 - 2 ln 3 + 1 6 .
Vậy a = - 2 , b = 3 , c = 1 6 → S = a + b + c = - 2 + 3 + 1 6 = 7 6 .
Đúng 0
Bình luận (0)
Cho tích phân
∫
2
3
1
x
3
+
x
2
d
x
a
ln
3
+
b
ln
2
+
c
với
a
,
b
,
c
∈
ℚ
. Tính tổng Sa+b+c A.
S...
Đọc tiếp
Cho tích phân ∫ 2 3 1 x 3 + x 2 d x = a ln 3 + b ln 2 + c với a , b , c ∈ ℚ . Tính tổng S=a+b+c
A. S = − 2 3
B. S = − 7 6
C. S = 2 3
D. S = 7 6
Cho tích phân
∫
2
3
1
x
3
+
x
2
d
x
a
ln
3
+
b
ln
2
+
c
với
a
,
b
,
c
∈...
Đọc tiếp
Cho tích phân ∫ 2 3 1 x 3 + x 2 d x = a ln 3 + b ln 2 + c với a , b , c ∈ ℚ . Tính tổng S = a + b + c

Cho hàm số f(x) xác định trên
(
-
∞
;
-
1
)
∪
(
0
;
+
∞
)
và
f
(
x
)
1
x
2
+
x
;
f
(
1
)
ln...
Đọc tiếp
Cho hàm số f(x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) và f ' ( x ) = 1 x 2 + x ; f ( 1 ) = ln 1 2 Biết ∫ 1 2 x 2 + 1 f ( x ) d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỉ. Giá trị biểu thức a+b+c bằng
A. 27/2
B. 1/6
C. 7/6
D. -3/2