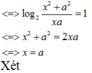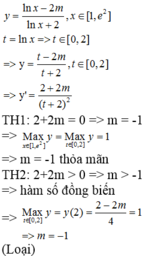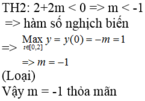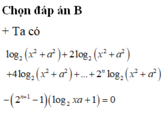Cho a,b là các số nguyên dương thỏa mãn a2+2010ab-4024b2=0.Tìm GTNN của: M=a2-3b2-2b+2017
TN
Những câu hỏi liên quan
Tìm số nguyên dương a,b thỏa mãn : a2 = 3b2
\(a^2=3b^2\)
Vì \(a^2;b^2\) là số chính phương
\(\Rightarrow a^2⋮̸3b^2\)
Nên không tồn tại a;b nguyên dương thỏa đẳng thức \(a^2=3b^2\)
Đúng 0
Bình luận (0)
Phần lỗi màu đỏ là a2 không thể chia cho 3 có thương là b2 là số chính phương
Đúng 0
Bình luận (0)
Cho a,b là các số thực dương thỏa mãn a2 -2ab -3b2 ≥ 0. Tìm giá trị nhỏ nhất P =\(\dfrac{4a^2+b^2}{ab}\)
Lời giải:
$a^2-2ab-3b^2\geq 0$
$\Leftrightarrow (a^2+ab)-(3ab+3b^2)\geq 0$
$\Leftrightarrow a(a+b)-3b(a+b)\geq 0$
$\Leftrightarrow (a+b)(a-3b)\geq 0$
$\Leftrightarrow a-3b\geq 0$ (do $a+b>0$ với mọi $a,b>0$)
$\Leftrightarrow a\geq 3b$
Xét hiệu:
$P-\frac{37}{3}=\frac{4a^2+b^2}{ab}-\frac{37}{3}$
$=\frac{12a^2+3b^2-37ab}{3ab}=\frac{(a-3b)(12a-b)}{3ab}\geq 0$ do $a\geq 3b>0$
$\Rightarrow P\geq \frac{37}{3}$
Vậy $P_{\min}=\frac{37}{3}$
Đúng 1
Bình luận (0)
Cho a,b là các số nguyên dương thỏa mãn a2+2010ab-4024b2=0.Tìm GTNN của: M=a2-3b2-2b+2017
Cho a, b là hai số nguyên dương thỏa mãn \(\dfrac{a+b^3}{a^2+3ab+3b^2-1}\) là một số nguyên. Chứng minh rằng a2 + 3ab + 3b2 - 1 chia hết cho lập phương của một số nguyên lớn hơn 1
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 ; e 2 y = 1 . Số phần tử của S là:/
A. 0
B. 1
C. 2
D. Vô số
Chọn B
Cách giải: Ta có:
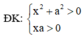
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
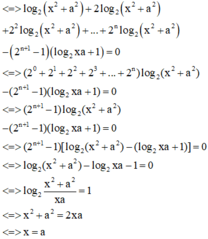
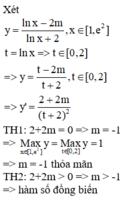
![]()
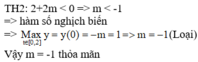
Đúng 0
Bình luận (0)
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số
cho a,b,c là 3 số dương thỏa mãn: a+b+c=2019. Tìm GTNN : a3/a2+b2+ab + b3/b2+c2+bc + c3/c2+a2+ca
Đặt \(P=\dfrac{a^3}{a^2+b^2+ab}+\dfrac{b^3}{b^2+c^2+bc}+\dfrac{c^3}{c^2+a^2+ca}\)
Ta có: \(\dfrac{a^3}{a^2+b^2+ab}=a-\dfrac{ab\left(a+b\right)}{a^2+b^2+ab}\ge a-\dfrac{ab\left(a+b\right)}{3\sqrt[3]{a^3b^3}}=a-\dfrac{a+b}{3}=\dfrac{2a-b}{3}\)
Tương tự: \(\dfrac{b^3}{b^2+c^2+bc}\ge\dfrac{2b-c}{3}\) ; \(\dfrac{c^3}{c^2+a^2+ca}\ge\dfrac{2c-a}{3}\)
Cộng vế:
\(P\ge\dfrac{a+b+c}{3}=673\)
Dấu "=" xảy ra khi \(a=b=c=673\)
Đúng 0
Bình luận (0)
Cho hàm số
y
ln
(
2
x
-
a
)
-
2
m
ln
(
2
x
-
a
)
+...
Đọc tiếp
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Cho a , b là hai số thực dương thỏa mãn
log
5
4
a
+
2
b
+
5
a
+
b
a
+
3
b
-
4
. Tìm giá trị nhỏ nhất của biểu thức
T...
Đọc tiếp
Cho a , b là hai số thực dương thỏa mãn log 5 4 a + 2 b + 5 a + b = a + 3 b - 4 . Tìm giá trị nhỏ nhất của biểu thức T = a 2 + b 2
A. 1 2
B. 1.
C. 3 2
D. 5 2
Ta có:
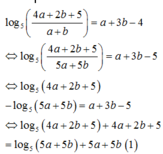
Xét hàm số
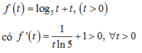
Hàm số f t đồng biến trên 0 ; + ∞
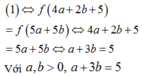
ta có:
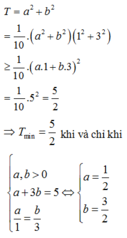
Chọn: D
Đúng 0
Bình luận (0)