A=10.12+12.14+14.16+16.18+18.2+20.22+22.2424.26+26.28+28.3+30.32+32.34+34.36

A=(12.14+34.36)+(14.16+32.34)+(16.18+30.32)+(18.2+28.3)+(20.22+26.28)+(22.24+24.26)

A=   46.5           +        46.5      +      46.5       +     46.5       +    46.5         +    46.5

A=                   93                    +                   93                   +                93

A=                                     93*3           = 279

A=10,12+12,14+14,16+16,18+...+32,34+34,36

A=(10+12+14+...+34)+(0,12+0,14+0,16+0,18+...+0,32+0,36)

A=286+3,12

A=289,12

A= 289,12 theo mình là đúng bạn thử xem có đúng không nhé

a,ƯCLN(24; 36)

Ta có:

24= 2³.3

36= 2.3³

Vậy: ƯCLN(24; 36)= 2.3= 6

ƯC( 24; 56)

Ta có:

Ư(24)= {1;2;3;4;6;8;12;24}

Ư(56)= {1;2;4;7;8;14;28;56}

ƯC(6; 8)={1;2;4;8}

b,BCNN(10; 12)

Ta có:

10=2.5

12=2².3

Vậy: BCNN(10; 12)=2².3.5=60

BC(10; 12)

Ta có:

B(10)={0;10;20;30;40;50;60;...}

B(12)={0;12;24;36;48;60;...}

BC(10; 12)={0;60;...}

tìm BC(10,12)

Tất nhiên là 30 rồi bạn ạ

thank tick cho cậu một cái

10,12+10,12=20,24

10,12+10,12=20,24

10,12 + 10,12 = 20,24

k minh di

A

Biết 12, ...4<12,14 Chữ số điền vào ô trống(viết rõ chỗ ra chứ)

A.0

B.1

C.2

D.3

A nhé

ChọnA

A

A em nhé

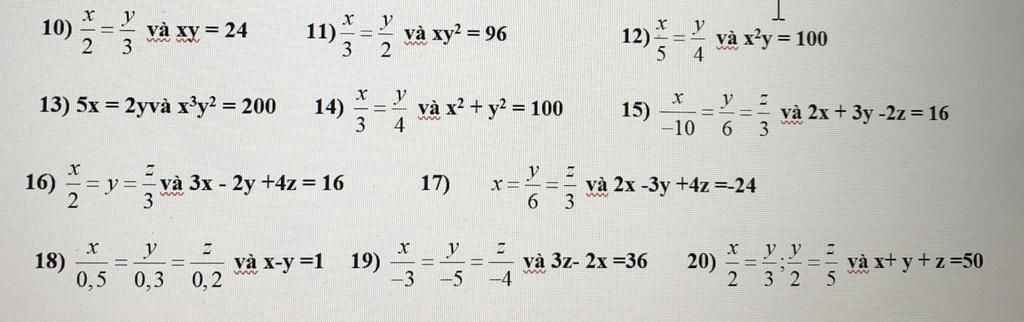
14) \(\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x^2}{3^2}=\dfrac{y^2}{4^2}\)

Theo tính chất của DTSBN, ta được :

\(\dfrac{x^2}{3^2}=\dfrac{y^2}{4^2}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)

\(\Rightarrow\left\{{}\begin{matrix}x^2=4.3^2=36\\y^2=4.4^2=64\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\pm6\\y=\pm8\end{matrix}\right.\)

Vì x,y cùng dấu nên cặp số (x ; y) = (6 ; 8) ; (-6 ; - 8)

12, Ta có : \(\dfrac{x}{5}=\dfrac{y}{4}\)

\(\Rightarrow y=\dfrac{4}{5}x\)

- Thay y vào biểu thức trên ta được ; \(\dfrac{4}{5}x^3=100\)

\(\Rightarrow x=5\)

\(\Rightarrow y=4\)

Vậy...

14, Ta có : \(\dfrac{x}{3}=\dfrac{y}{4}\)

\(\Rightarrow\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{25}=4\) ( Tính chất dãy tỉ số bằng nhau )

\(\Rightarrow\left\{{}\begin{matrix}x=\pm6\\y=\pm8\end{matrix}\right.\)

Vậy ...

16) Ta có: \(\dfrac{x}{2}=y=\dfrac{z}{3}\)

\(\Leftrightarrow\dfrac{x}{2}=\dfrac{y}{1}=\dfrac{z}{3}\)

\(\Leftrightarrow\dfrac{3x}{6}=\dfrac{2y}{2}=\dfrac{4z}{12}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{3x}{6}=\dfrac{2y}{2}=\dfrac{4z}{12}=\dfrac{3x-2y+4z}{6-2+12}=\dfrac{16}{16}=1\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{x}{2}=1\\y=1\\\dfrac{z}{3}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\\z=3\end{matrix}\right.\)

=23

=23