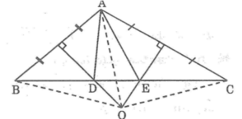
Cho tam giác ABC có Góc A là góc tù. Các đường trung trực của AB;AC cắt nhau tại O và lần lượt cắt BC tại M,N. CMR AO là tia phân giác của góc MAN
Cho tam giác ABC có góc A là góc tù. Các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở D và E. Các tam giác ABD, ACE là tam giác gì?
Vì D thuộc đường trung trực của AB nên:
DA = DB (tính chất đường trung trực)
Suy ra: ΔADB cân tại D.
Vì E thuộc đường trung trực của AC nên:
EA = EC (tính chất đường trung trực)
Suy ra: ΔAEC cân tại E.
Cho tam giác ABC có góc A là góc tù. Các đường trung trực của AB ; AC cắt nhau tại O và lần lượt cắt BC tại M, N. Chứng minh rằng AO là phân giác của góc MAN
Cho tam giác ABC có góc A là góc tù. Các đường trung trực của AB; AC cắt nhau tại O và lần lượt cắt BC tại M, N. Chứng minh rằng AO là tia phân giác của góc MAN.
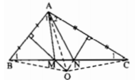
Theo bài 8.3 ta đã có ∠A1 = ∠B1 , ∠A2 = ∠C2 (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra ∠(OAB) = ∠(OBA) , ∠(OAC) = ∠(OCA) , ∠(OBC) = ∠(OCB) . Kết hợp với(1) ∠(OBM) = ∠(OAM) , ∠(OCN) = ∠(OAN) , hay ∠(OAM) = ∠(OBC) = ∠(OCB) = ∠(OAN). Vậy OA là tia phân giác góc MAN.
Cho tam giác ABC có góc A là góc tù. Các đường trung trực AB; AC cắt nhau tại O và lần lượt cắt BC tại M, N. Chứng minh rằng AO là tia phân giác của góc MAN ?
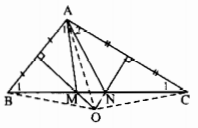
Theo bài 8.3 ta đã có\(\widehat{A_1} =\widehat{B}_1;\widehat{A_2}=\widehat{C_1} \) (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra \(\widehat{OAB}=\widehat{OBA},\widehat{OAC}=\widehat{OCA},\widehat{OCB}=\widehat{OBC}\)Kết hợp với (1) \(\widehat{OBM}=\widehat{OAM},\widehat{OCN}=\widehat{OAN}\) hay\(\widehat{OAM}=\widehat{OBC}=\widehat{OCB}=\widehat{OAN}\) . Vậy OA là tia phân giác góc MAN.
Hình thì bạn kia vẽ rồi nên mình không vẽ nữa nha
Theo bài 8.3 ta đã cóˆA1=ˆB1;ˆA2=ˆC1A1^=B^1;A2^=C1^ (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra ˆOAB=ˆOBA,ˆOAC=ˆOCA,ˆOCB=ˆOBCOAB^=OBA^,OAC^=OCA^,OCB^=OBC^Kết hợp với (1) ˆOBM=ˆOAM,ˆOCN=ˆOANOBM^=OAM^,OCN^=OAN^ hayˆOAM=ˆOBC=ˆOCB=ˆOANOAM^=OBC^=OCB^=OAN^ . Vậy OA là tia phân giác góc MAN.
a) Vẽ tam giác ABC có góc A là góc tù. Vẽ đường trung trực của các cạnh AB,BC,AC
b) Cho tam giác ABC có góc A=90 độ, có AC=9cm,BC=24cm. Vẽ đường thẳng d là đường trung trực của đoạn thẳng BC cắt tia CA
GIÚP MÌNH VỚI NHA
cho tam giác abc có góc a tù. các đường trung trực của Ab và AC cắt nhau tại O và cắt BC theo thứ tự là M và N. chứng minh rằng AO là tia phân giác của góc MAN
Cho tam giác ABC (góc A tù) đường cao AI.Biết rằng O là giao điểm của 3 đường phân giác của tam giác ABC nằm trên AI.H là giao điểm của 3 đường trung trực của tam giác ABC.H nằm trên AI và BC là đường trung trực của đoạn thẳng OH.Tính các góc của tam giác ABC
Tam giác ABC có góc A là góc tù. Các đường trung trực của các cạnh AB và AC cắt nhau ở O. Các điểm B và C có thuộc đường tròn tâm O bán kính OA hay không? Vì sao?
Từ giả thiết suy ra OA = OB = OC.
Vậy các điểm B và C có thuộc đường tròn tâm O bán kính OA.
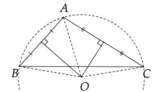
Cho tam giác abc có góc a tù. các đường trung trực của Ab và AC cắt nhau tại O và cắt BC theo thứ tự là M và N. chứng minh rằng AO là tia phân giác của góc MAN.