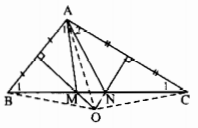
Theo bài 8.3 ta đã có\(\widehat{A_1} =\widehat{B}_1;\widehat{A_2}=\widehat{C_1} \) (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra \(\widehat{OAB}=\widehat{OBA},\widehat{OAC}=\widehat{OCA},\widehat{OCB}=\widehat{OBC}\)Kết hợp với (1) \(\widehat{OBM}=\widehat{OAM},\widehat{OCN}=\widehat{OAN}\) hay\(\widehat{OAM}=\widehat{OBC}=\widehat{OCB}=\widehat{OAN}\) . Vậy OA là tia phân giác góc MAN.
Hình thì bạn kia vẽ rồi nên mình không vẽ nữa nha
Theo bài 8.3 ta đã cóˆA1=ˆB1;ˆA2=ˆC1A1^=B^1;A2^=C1^ (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra ˆOAB=ˆOBA,ˆOAC=ˆOCA,ˆOCB=ˆOBCOAB^=OBA^,OAC^=OCA^,OCB^=OBC^Kết hợp với (1) ˆOBM=ˆOAM,ˆOCN=ˆOANOBM^=OAM^,OCN^=OAN^ hayˆOAM=ˆOBC=ˆOCB=ˆOANOAM^=OBC^=OCB^=OAN^ . Vậy OA là tia phân giác góc MAN.

