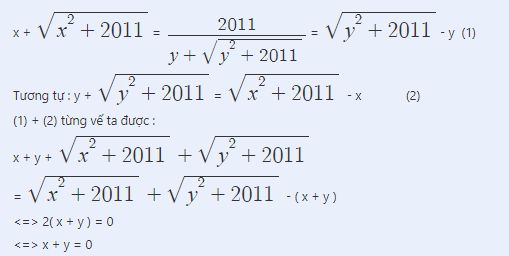cho 2 số a và b thõa mãn a+b/2=1 tính giá trị lớn nhất của biểu thức 2011/2a^2+2b^2+2008
KK
Những câu hỏi liên quan
Cho a, b thõa mãn \(\frac{a+b}{2}=1\). Tính giá trị lớn nhất của biểu thức \(\frac{2011}{2a^2+2b^2+2008}\).
Ta có :\(\left(a-b\right)^2\ge0\forall a;b\Leftrightarrow a^2-2ab+b^2\ge0\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow2a^2+2b^2\ge a^2+b^2+2ab\Leftrightarrow2a^2+2b^2\ge\left(a+b\right)^2\)
Suy ra \(\frac{2011}{2a^2+2b^2+2008}\le\frac{2011}{\left(a+b\right)^2+2008}=\frac{2011}{4+2008}=\frac{2011}{2012}\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=1\)
Đúng 0
Bình luận (0)
a) Cho (x+\(\sqrt{x^2+2011}\)).(y+\(\sqrt{y^2+2011}\))=2011.Tính x+y
b) Với a,b,c là các số dương thỏa mãn điều kiện a+b+c=2 .Tìm giá trị lớn nhất của biểu thức Q=\(\sqrt{2a+bc}+\sqrt{2b+ca}+\sqrt{2c+ab}\)
b)
https://hoc24.vn/cau-hoi/c-voi-a-b-c-la-cac-so-duong-thoa-man-dieu-kien-a-b-c-2-tim-max-q-sqrt2abcsqrt2bcasqrt2cab.8298826302
Bạn có thể tham khảo ở đây. Đừng quên like giúp mik nha bạn. Thx
Đúng 1
Bình luận (0)
Cho hai số thực a,b khác 0 thõa mãn \(2a^2+\frac{b^2}{4}+\frac{1}{a^2}=4\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức S=ab+2019
\(2a^2+\frac{1}{a^2}+\frac{b^2}{4}=4\Leftrightarrow\left(a^2+\frac{1}{a^2}-2\right)+\left(a^2+\frac{b^2}{4}-ab\right)=4-ab-2\)
\(\Leftrightarrow\left(a-\frac{1}{a}\right)^2+\left(a-\frac{b}{2}\right)^2=2-ab\)
\(VF=2-ab=\left(a-\frac{1}{a}\right)^2+\left(b-\frac{b}{2}\right)^2\ge0\)
Hay \(ab\le2\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}a=\frac{1}{a}\\b=\frac{b}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}\left(a;b\right)=\left(1;\frac{1}{2}\right)\\\left(a;b\right)=\left(-1;-\frac{1}{2}\right)\end{cases}}\)
Đúng 0
Bình luận (0)
ủa bạn tìm giá trị nhỏ nhất của biểu thức S=ab+2019 mà
Đúng 0
Bình luận (0)
cho 2 số a,b thỏa mãn \(\dfrac{a+b}{2}\)
Tính giá trị lớn nhất của biểu thức: \(\dfrac{2011}{2a^2+2b^2+2008}\)
giúp mk câu ni vs::cho các số dương a,b,c thõa mãn ab+bc+ac=1. Tìm giá trị lớn nhất của biểu thức P= 2a/căn(1+a^2) +b/căn(1+b^2)+c/căn(1+c^2)
Áp dụng BĐT Cauchy-Schwarz ta có:
\(P=\frac{2a}{\sqrt{1+a^2}}+\frac{b}{\sqrt{1+b^2}}+\frac{c}{\sqrt{1+c^2}}\)
\(=\frac{2a}{\sqrt{\left(a+b\right)\left(a+c\right)}}+\frac{b}{\sqrt{\left(a+b\right)\left(b+c\right)}}+\frac{c}{\sqrt{\left(a+c\right)\left(b+c\right)}}\)
\(=\sqrt{\frac{2a}{a+b}\cdot\frac{2a}{a+c}}+\sqrt{\frac{2b}{a+b}\cdot\frac{b}{2\left(b+c\right)}}+\sqrt{\frac{2c}{a+c}\cdot\frac{c}{2\left(b+c\right)}}\)
\(\le\frac{1}{2}\left(\frac{2a}{a+b}+\frac{2b}{a+b}+\frac{2a}{a+c}+\frac{2c}{a+c}+\frac{b}{2\left(b+c\right)}+\frac{c}{2\left(b+c\right)}\right)\)
\(=\frac{1}{2}\left(2+2+\frac{1}{2}\right)=\frac{9}{4}\)
Đúng 0
Bình luận (0)
Áp dụng BĐT Cauchy-Schwarz ta có :
\(P=\frac{2a}{\sqrt{1+a^2}}+\frac{b}{\sqrt{1+b^2}}+\frac{c}{\sqrt{1+c^2}}\)
\(=\frac{2a}{\sqrt{\left(a+b\right)\left(a+c\right)}}+\frac{b}{\sqrt{\left(a+b\right)\left(b+c\right)}}+\frac{c}{\sqrt{\left(a+c\right)\left(b+c\right)}}\)
\(=\sqrt{\frac{2a}{a+b}.\frac{2a}{a+c}}+\sqrt{\frac{2b}{a+b}.\frac{b}{2\left(b+c\right)}}+\sqrt{\frac{2c}{a+c}.\frac{c}{2\left(b +c\right)}}\)
\(\le\frac{1}{2}\left(\frac{2a}{a+b}+\frac{2b}{a+b}+\frac{2a}{a+c}+\frac{2c}{a+c}+\frac{b}{2\left(b+c\right)}+\frac{c}{2\left(b+c\right)}\right)\)
\(=\frac{1}{2}\left(2+2+\frac{1}{2}\right)=\frac{9}{4}\)
P/s : Mình tự nghĩ chứ không phải mình copy đâu
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a/\(Cho\) \(a,b\) \(\ne0\) \(thõa\) \(mãn\) \(2a=3b\) .Tính giá trị của biểu thức:\(M=\dfrac{a^3-2ab^2+b^3}{a^2b+ab^2+b^3}\)
b/Chứng minh một số tự nhiên có tổng các chữ số là 20142015 không phải là số chính phương
a/ Ta có: `2a = 3b => a/3 = b/2`
Đặt `a/3 = b/2 = k` \(\left(k\ne0\right)\)
`=> a = 3k ; b = 2k`
`=> M =`\(\dfrac{\left(3k\right)^3-2.3k.\left(2k\right)^2+\left(2k\right)^3}{\left(3k\right)^2.2k+3k.\left(2k\right)^2+\left(2k\right)^3}=\dfrac{27k^3-24k^3+8k^3}{18k^3+12k^3+8k^3}=\dfrac{11k^3}{38k^3}=\dfrac{11}{38}\)
Vậy `M = 11/38`.
b/ Giả sử tồn tại số chính phương `a^2` có tổng các số tự nhiên là 20142015
Vì \(20142015⋮3\) nên \(a^2⋮3\)
\(\Rightarrow a^2⋮3^2\)
\(\Rightarrow a^2⋮9\)
Mà \(20142015⋮9̸\Rightarrow a^2⋮9̸\) (vô lí)
`=>` Không tồn tại số chính phương `a^2` nào có tổng các số tự nhiên là 20142015
\(\Rightarrow\) 1 số tự nhiên có tổng các chữ số là `20142015` không phải là số chính phương (đpcm)
Đúng 1
Bình luận (0)
cho 2 số a và b thoả mãn a+b/2=1 tính giá trị lớn nhất M= 2020/2a^2+2b^2+2019
cho 2 số a,b thỏa mãn \(\dfrac{a+b}{2}\)=1 . tính giá trị lớn nhất của biểu thức \(\dfrac{2011}{2a^2+2b^2+2008}\)
mình đag cần gấp mong các bạn giúp cho ạ
Đặt \(Q=\dfrac{2011}{2a^2+2b^2+2008}\)
Ta có:
\(\dfrac{a+b}{2}=1=>a+b=2=>a=2-b\)
Thay a=2-b vào Q ta được:
\(Q=\dfrac{2011}{2a^2+2\left(2-a\right)^2+2008}\)
=\(\dfrac{2011}{2a^2+2\left(4-4a+a^2\right)+2008}\)
=\(\dfrac{2011}{2a^2+8-8a+2a^2+2008}\)
=\(\dfrac{2011}{4a^2-8a+2016}\)
=\(\dfrac{2011}{4a^2-8a+4+2012}\)
=\(\dfrac{2011}{4\left(a^2-2a+1\right)+2012}\)
=\(\dfrac{2011}{4\left(a-1\right)^2+2012}\)
Vì \(2a^2+2b^2+2008>0với\forall a,b\)
nên để Q đạt GTLN thì \(2a^2+2b^2+2008\)đạt GTNN hay \(4\left(a-1\right)^2+2012\)đạt GTNN
Mặt khác \(4\left(a-1\right)^2\)\(\ge\)0 với \(\forall\)a
Do đó\(4\left(a-1\right)^2+2012\) \(\ge\)0 với \(\forall\)a
Dấu "=" xảy ra <=> a-1=0<=>a=1
Mà a+b=2=>b=1
Vậy GTN của \(Q=\dfrac{2011}{2a^2+2b^2+2008}\)là \(\dfrac{2011}{2012}\)khi a=b=1
Đúng 0
Bình luận (0)
Cách 2 :
Ta có : \(\dfrac{a+b}{2}=1\Rightarrow a+b=2\)
Mặt khác : Với \(\forall a,b\) thì : \(a^2+b^2\ge2ab\)
\(\Rightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2=4\)
\(\Rightarrow2a^2+2b^2+2008\ge2012\)
\(\Rightarrow\dfrac{2011}{2a^2+2b^2+2008}\le\dfrac{2011}{2012}\)
Dấu '' = '' xảy ra khi a = b = 1
Vậy GTLN của biểu thức là \(\dfrac{2011}{2012}\Leftrightarrow a=b=1\)
Đúng 0
Bình luận (2)
Cho ba số thực dương a,b,c thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
b
-
6
c
10
và a + c2 . Tính giá trị biểu thức P 3a + 2b + c khi
Q
a
2
+
b...
Đọc tiếp
Cho ba số thực dương a,b,c thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 b - 6 c = 10 và a + c=2 . Tính giá trị biểu thức P = 3a + 2b + c khi Q = a 2 + b 2 + c 2 - 14 a - 8 b + 18 c đạt giá trị lớn nhất.
A. 10
B. -10
C. 12
D. -12
Đáp án D

Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất





Đúng 0
Bình luận (0)