Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ y=2x+4 và y=-x-1
TL
Những câu hỏi liên quan
cho hàm số y = 2x+2 có đồ thhij là (d) và hàm số y = -x-1 có đồ thị là (d1)
a, vẽ (d) và (d1) trên cùng 1 mặt phẳng tọa độ trên tọa độ giao điểm của (d) và (d1) bằng phép toán
b, cho hàm số y=(m^2-11) x+m-5 (m là hàm số) co đò thị là (d2).tìm m để đt (d2) cắt đt (d).tìm m dể đt (d2) song song với đường thẳng (d)
Cho hai hàm số y x2/2 có đồ thị (P) và y -x + m có đồ thị (Dm).1. Với m 4, vẽ (P) và (D4) trên cùng một hệ trục tọa độ vuông góc Oxy. Xác định tọa độ các giao điểm của chúng.2. Xác định giá trị của m để:a) (Dm) cắt (P) tại điểm có hoành độ bằng 1.b) (Dm) cắt (P) tại 2 điểm phân biệt.c) (Dm) tiếp xúc (P). Xác định tọa độ tiếp điểm.
Đọc tiếp
Cho hai hàm số y = x2/2 có đồ thị (P) và y = -x + m có đồ thị (Dm).
1. Với m = 4, vẽ (P) và (D4) trên cùng một hệ trục tọa độ vuông góc Oxy. Xác định tọa độ các giao điểm của chúng.
2. Xác định giá trị của m để:
a) (Dm) cắt (P) tại điểm có hoành độ bằng 1.
b) (Dm) cắt (P) tại 2 điểm phân biệt.
c) (Dm) tiếp xúc (P). Xác định tọa độ tiếp điểm.
2:
a: Thay x=1 vào (P), ta được:
\(y=\dfrac{1^2}{2}=\dfrac{1}{2}\)
Thay x=1 và y=1/2 vào (D), ta được:
\(m-1=\dfrac{1}{2}\)
hay m=3/2
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2+x-m=0\)
\(\text{Δ}=1^2-4\cdot\dfrac{1}{2}\cdot\left(-m\right)=2m+1\)
Để (D) cắt (P) tại hai điểm phân biệt thì 2m+1>0
hay m>-1/2
c: Để (D) tiếp xúc với (P) thì 2m+1=0
hay m=-1/2
Đúng 0
Bình luận (0)
Vẽ trên cùng một hệ trục tọa độ Oxy đồ thị của các hàm số:
a) y=x; b) y=3x; c) y=-2x; d) y=-x
a) trong mặt phẳng oxy , vẽ đồ thị hàm số y = -2x
b) Tìm tọa độ điểm B , biết B thuộc đồ thị hàm số trên và B có tung độ là 4
chỉ cần câu b thôi ko cần câu a
a/ vẽ đồ thị của các hàm số y= x+1 và y= -x+3 trên cùng một mặt phẳn tọa độ.
b/ Hai đường thẳng y=x+1 và y=-x+3 cắt nhau tại C và cắc trục Ox theo thứ tự A và B. Tìm tọa độ các điểm A, B, C.
c/ Tính chu vi và diện tích tam giác ABC ( đơn vị đo trên trục tọa độ là xentimet)
Bài 6. Cho hàm số y = -2x + 3.
a) Vẽ đồ thị của hàm số trên.
b) Gọi A và B theo thứ tự là giao điểm của đồ thị với các trục Ox và Oy. Tính diện tích tam giác OAB (với O là gốc tọa độ và đơn vị trên các trục tọa độ là centimet ).
c) Tính độ dài đoạn AB
\(b,\text{PT giao Ox và Oy: }\\ y=0\Leftrightarrow x=\dfrac{3}{2}\Leftrightarrow A\left(\dfrac{3}{2};0\right)\Leftrightarrow OA=\dfrac{3}{2}\\ x=0\Leftrightarrow y=3\Leftrightarrow B\left(0;3\right)\Leftrightarrow OB=3\\ \Leftrightarrow S_{OAB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\cdot\dfrac{3}{2}\cdot3=\dfrac{9}{4}\left(cm^2\right)\\ c,C_1:\text{Áp dụng Pytago: }AB=\sqrt{OA^2+OB^2}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\\ C_2:AB=\sqrt{\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2}=\sqrt{\left(\dfrac{3}{2}-0\right)^2+\left(0-3\right)^2}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\)
Đúng 2
Bình luận (1)
Cho hàm số sau d:y= x+2
a) Vẽ đồ thị hàm số trên mặt phẳng tọa độ Oxy
b)Gọi A,B là giao điểm của d với Ox, Oy. Tính diện tích tam giác OAB
c)Tính góc tạo bởi d và trục Ox
a: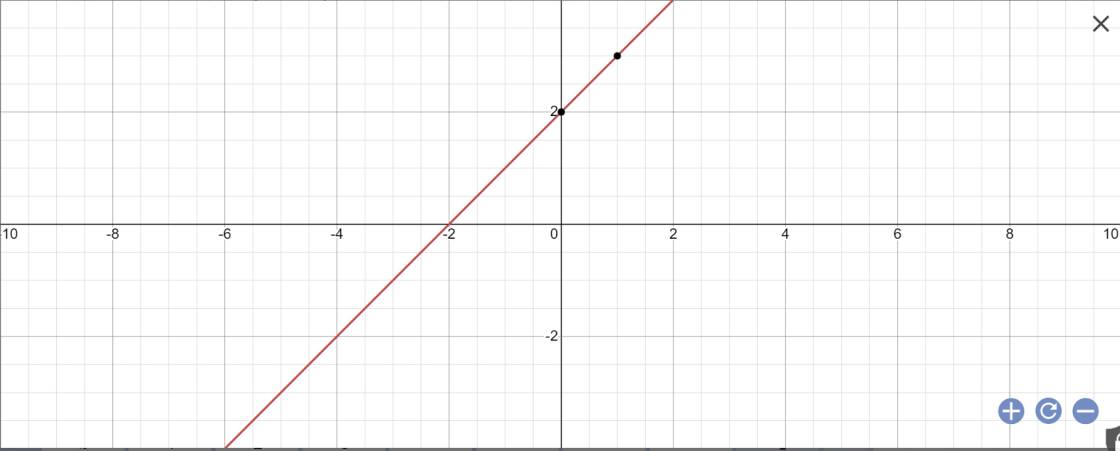 
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\)
Ox\(\perp\)Oy
mà \(A\in Ox,B\in Oy\)
nên OA\(\perp\)OB
=>ΔOAB vuông tại O
O(0;0); A(-2;0); B(0;2)
\(OA=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{4}=2\)
\(OB=\sqrt{\left(0-0\right)^2+\left(2-0\right)^2}=2\)
ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot AO\cdot OB=\dfrac{1}{2}\cdot2\cdot2=2\)
c: Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
(d): y=x+2
=>a=1
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
Đúng 1
Bình luận (0)
Cho hàm số y= -2x - 4 (d) và y= x +4 (d')
a) Vẽ đồ thị hai hàm số trên cùng mặt phẳng toạ độ ?
b) Gọi giao điểm của đường thẳng (d) và (d') với trục Oy lằn lượt là A;B và gọi giao điểm của hai ₫ường thẳng là C . Xác định toạ độ điểm C và tính diện tích tam giác ABC
c) Tính các góc của tam giác ABC
vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số
a y=-x b)y=1/2 x c)y=-1/2x
vd x=2
thì:
a. y=-x
=> y=-2
b. y=1/2x
=> y=1/2.2
=> y=1
c. y=-1/2x
=> y=-1/2.2
=> y=-1
Đúng 0
Bình luận (0)