tạo chương trình vẽ hình vuông với độ dài mỗi cạnh là 50 đơn vị
PA
Những câu hỏi liên quan
Hình vuông có độ dài bé hơn 4m.Tính chu vi mỗi hình vuông,biết răng độ dài cạnh là số tự nhiên với đơn vị là mét
chu vi hình vuông cạnh 3m là
3x4=12(m)
chu vi cạnh là 2 m là
2x4=8(m)
chu vi hình vuông cạnh 1 m là
1x4=4(m)
Đúng 0
Bình luận (0)
Hình vuông có độ dài acnhj bé hơn là 4m.Tính chu vi mỗi hình vuông,biết rằng độ dài cạnh là số tự nhiên với đơn vị là mét
ML
SGK Cánh diều - Trang 98
24 tháng 7 2023 lúc 17:21
Vòng lặp ở Hình 5 sẽ làm nhân vật vẽ một hình vuông với các cạnh có màu khác nhau. Em hãy tạo chương trình vẽ Hình 6.
Gợi ý: Hãy lặp lại việc vẽ hình vuông 12 lần, nhưng sau mỗi lần vẽ xong một hình vuông thì xoay hướng nhân vật vẽ 30o trước khi vẽ hình vuông tiếp theo.
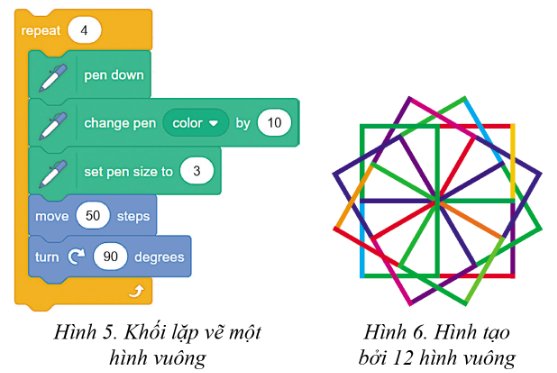
- Sử dụng vòng lặp với số lần lặp là 12
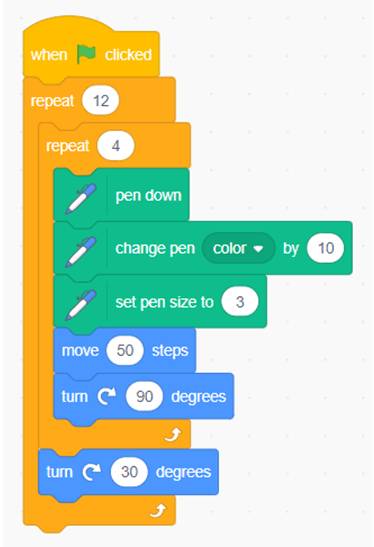
Kết quả thu được là
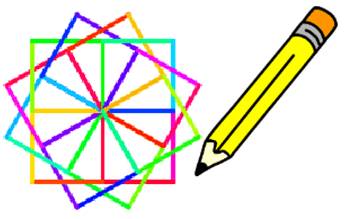
Đúng 1
Bình luận (0)
Một đấm đất hình chữ nhật dài 36m, rộng 24m. Người ta muốn chia đám đất thành những ô vuông bằng nhau, lớn nhất. Hỏi cạnh của mỗi ô vuông là bao nhiêu? (độ dài mỗi cạnh là một số tự nhiên với đơn vị là mét)
\(36=2^2\cdot3^2;24=2^3\cdot3\)
=>\(ƯCLN\left(36;24\right)=2^2\cdot3=12\)
Để chia đám đất hình chữ nhật dài 36m, rộng 24m thành những ô vuông bằng nhau và lớn nhất thì độ dài cạnh của các ô vuông phải là ước chung lớn nhất của 36 và 24
=>Độ dài cạnh của ô vuông là 12m
Đúng 1
Bình luận (0)
Một mảnh đất hình chữ nhật dài 36m, rộng 24m. Người ta muốn chia mảnh đất thành những ô vuông bằng nhau. Hỏi độ dài cạnh ô vuông lớn nhất có thể chia là bao nhiêu? (Độ dài mỗi cạnh là một số tự nhiên với đơn vị là mét)
Số ô vuông lớn nhất có thể chia là: 12 ô
Đúng 0
Bình luận (0)
H24
trang 50 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 10:29
Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đỏ từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?
Ta có: \({u_1} = 1;{u_2} = 1;{u_3} = 2;{u_4} = 3;{u_5} = 5;{u_6} = 8;{u_7} = 13;{u_8} = 21\)
Ta có:
\(\begin{array}{l}{u_3} = 2 = {u_2} + {u_1}\\{u_4} = 3 = {u_3} + {u_2}\\{u_5} = 5 = {u_4} + {u_3}\\{u_6} = 8 = {u_5} + {u_4}\\{u_7} = 13 = {u_6} + {u_5}\\{u_8} = 21 = {u_7} + {u_6}\end{array}\)
Ta thấy dãy số này kể từ số hạng thứ 3 bằng tổng của hai số hạng đứng trước nó.
Vậy dãy số này có công thức truy hồi là:
\(\left\{ \begin{array}{l}{u_1} = 1;{u_2} = 1\\{u_n} = {u_{n - 1}} + {u_{n - 2}}\left( {n \ge 3} \right)\end{array} \right.\)
Đúng 0
Bình luận (0)
H24
trang 69 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 12:52
Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:Bắt đầu bằng một hình vuông {H_0} cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông {H_0} thành chính hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình {H_1} (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của {H_1} thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình {H_2} (xem Hình 6c). Tiếp tục quá trình này, ta nhận được một dãy hình {H_n}left( {n 1,2,3,...} right).Ta có: {H_1} có 5 hình vuông,...
Đọc tiếp
Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:
Bắt đầu bằng một hình vuông \({H_0}\) cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông \({H_0}\) thành chính hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình \({H_1}\) (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của \({H_1}\) thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình \({H_2}\) (xem Hình 6c). Tiếp tục quá trình này, ta nhận được một dãy hình \({H_n}\left( {n = 1,2,3,...} \right)\).
Ta có: \({H_1}\) có 5 hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}\);
\({H_2}\) có \(5.5 = {5^2}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}.\frac{1}{3} = \frac{1}{{{3^2}}}\);…
Từ đó, nhận được hình \({H_n}\) có \({5^n}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{{{3^n}}}\).
a) Tính diện tích \({S_n}\) của \({H_n}\) và tính \(\lim {S_n}\).
b) Tính chu vi \({p_n}\) của \({H_n}\) và tính \(\lim {p_n}\).
(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích \(\lim {S_n}\) và chu vi \(\lim {p_n}\)).
a) \({S_n} = {5^n}.{\left( {\frac{1}{{{3^n}}}} \right)^2} = {5^n}.\frac{1}{{{9^n}}} = {\left( {\frac{5}{9}} \right)^n},n = 1,2,3,...\)
\(\lim {S_n} = \lim {\left( {\frac{5}{9}} \right)^n} = 0\)
b) \({p_n} = {5^n}.4.\frac{1}{{{3^n}}} = 4.{\left( {\frac{5}{3}} \right)^n},n = 1,2,3,...\)
\(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right)\)
Vì \(\lim \frac{1}{{4.{{\left( {\frac{5}{3}} \right)}^n}}} = \frac{1}{4}.\lim {\left( {\frac{3}{5}} \right)^n} = 0\) và \(4.{\left( {\frac{5}{3}} \right)^n} > 0\) với mọi \(n\) nên \(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right) = + \infty \).
Đúng 0
Bình luận (0)
Viết chương trình nhập vào độ dài cạnh hình vuông, tính và đưa ra màn hình chu vi và diện tích hình vuông
(độ dài cạnh hình vuông, chu vi, diện tích là các số thực).
Bài 1. Một đám đất hình chữ nhật dài 36m, rộng 24m. Người ta muốn chia đám đất
thành những ô vuông bằng nhau, lớn nhất. Hỏi cạnh của mỗi ô vuông là bao nhiêu? (
Độ dài mỗi cạnh là một số tự nhiên với đơn vị là mét)
một hình vuông có số đo diện tích là một số tự nhiên gồm 4 chữ số với đơn vị là m2. Mà 2 chữ số đầu và hai chữ số cuối giống nhau. Tính độ dài cạnh của hình vuông dố biết độ dài cạnh là một số tự nhiên với đơn vị là mét