a)   S   =   32 ;   P   =   231   ⇒   S 2   –   4 P   =   322   –   4 . 231   =   100   >   0

⇒ Tồn tại u và v là hai nghiệm của phương trình:  x 2   –   32 x   +   231   =   0 .

Ta có:  Δ   =   ( - 32 ) 2   –   4 . 231   =   100   >   0

⇒ PT có hai nghiệm:

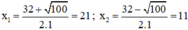
Vậy u = 21 ; v = 11 hoặc u = 11 ; v = 21.

b) S = -8; P = -105  ⇒   S 2   –   4 P   =   ( - 8 ) 2   –   4 . ( - 105 )   =   484   >   0

⇒ u và v là hai nghiệm của phương trình:  x 2   +   8 x   –   105   =   0

Ta có:  Δ ’   =   4 2   –   1 . ( - 105 )   =   121   >   0

Phương trình có hai nghiệm:

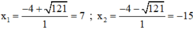
Vậy u = 7 ; v = -15 hoặc u = -15 ; v = 7.

c) S = 2 ; P = 9 ⇒  S 2   –   4 P   =   2 2   –   4 . 9   =   - 32   <   0

⇒ Không tồn tại u và v thỏa mãn.

Tức là như thế này:

a/ \(u+v=32\Rightarrow u=32-v\)hoặc \(v=32-u\)(Cái này tùy bạn chọn nhưng mình chọn cái 1)

Ta có: \(uv=231\)

\(\Leftrightarrow\left(32-v\right)v=231\)

\(\Leftrightarrow32v-v^2-231=0\)

\(\Leftrightarrow-v^2+32v-231=0\)

Sau đó bạn giải \(\Delta\)tìm được \(v\)và có \(v\)rồi thì ra cái còn lại.

Các câu sau tương tự không có gì hết

a) từ tổng u+v=32 => u=32-v rồi thay u=32-v vào uv=231 sẽ tìm ra u;v

các câu sau làm tương tự

Khó hiểu quá bạn ơi

a) u và v là nghiệm của phương trình: x² – 32x + 231 = 0

∆’ = 16² – 231 = 256 – 231 = 25, \(\sqrt{\text{∆}'}\) = 5 . x₁ = 21, x₂ = 11

Vậy u = 21, v = 11 hoặc u = 11, v = 21

b) u, v là nghiệm của phương trình:

x² + 8x – 105 = 0, ∆’ = 16 + 105 = 121, \(\sqrt{\text{∆}'}\) = 11 . x = -4 + 11 = 7

x₂ = -4 – 11 = -15

Vậy u = 7, v = -15 hoặc u = -15, v = 7

c) Vì 2² – 4 . 9 < 0 nên không có giá trị nào của u và v thỏa mãn điều kiện đã cho.

a) u và v là nghiệm của phương trình: x2 – 32x + 231 = 0

∆’ = 162 – 231 = 256 – 231 = 25, √∆' = 5 . x1 = 21, x2 = 11

Vậy u = 21, v = 11 hoặc u = 11, v = 21

b) u, v là nghiệm của phương trình:

x2 + 8x – 105 = 0, ∆’ = 16 + 105 = 121, √∆' = 11 . x = -4 + 11 = 7

x2 = -4 – 11 = -15

Vậy u = 7, v = -15 hoặc u = -15, v = 7

c) Vì 22 – 4 . 9 < 0 nên không có giá trị nào của u và v thỏa mãn điều kiện đã cho.

S = 2 ; P = 9 ⇒ S2 – 4P = 22 – 4.9 = -32 < 0

⇒ Không tồn tại u và v thỏa mãn.

\(u^2-22u+9\\ v^2-22v+9\)

\(B=\dfrac{2u+\sqrt{uv}-3v}{2u-5\sqrt{uv}+3v}\)

\(=\dfrac{2u+3\sqrt{uv}-2\sqrt{uv}-3v}{2u-2\sqrt{uv}-3\sqrt{uv}+3v}\)

\(=\dfrac{\sqrt{u}.\left(2\sqrt{u}+3\sqrt{v}\right)-\sqrt{v}.\left(2\sqrt{u}+3\sqrt{v}\right)}{2\sqrt{u}.\left(\sqrt{u}-\sqrt{v}\right)-3\sqrt{v}.\left(\sqrt{u}-\sqrt{v}\right)}\)

\(=\dfrac{\left(2\sqrt{u}+3\sqrt{v}\right)\left(\sqrt{u}-\sqrt{v}\right)}{\left(\sqrt{u}-\sqrt{v}\right)\left(2\sqrt{u}-3\sqrt{v}\right)}\)

\(=\dfrac{2\sqrt{u}+3\sqrt{v}}{2\sqrt{u}-3\sqrt{v}}\\ =\dfrac{4u+12\sqrt{uv}+9v}{4u-9v}\)

Phát biểu D đúng.

Cái này theo công thức đạo hàm thôi

Chọn D

a) S = 42; P = 441  ⇒   S 2   –   4 P   =   42 2   –   4 . 441   =   0

⇒ u và v là hai nghiệm của phương trình:  x 2   –   42 x   +   441   =   0

Có:   Δ ’   =   ( - 21 ) 2   –   441   =   0

⇒ Phương trình có nghiệm kép  x 1   =   x 2   =   - b ’ / a   =   21 .

Vậy u = v = 21.

b) S = -42; P = -400  ⇒   S 2   –   4 P   =   ( - 42 ) 2   –   4 . ( - 400 )   =   3364   >   0

⇒ u và v là hai nghiệm của phương trình:  x 2   +   42 x   –   400   =   0

Có  Δ ’   =   21 2   –   1 . ( - 400 )   =   841

⇒ Phương trình có hai nghiệm phân biệt:

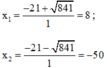
Vậy u = 8; v = -50 hoặc u = -50; v = 8.

c) u – v = 5 ⇒ u + (-v) = 5

u.v = 24 ⇒ u.(-v) = -uv = -24.

Ta tìm u và –v. Từ đó, ta dễ dàng tính được u và v.

S= u + (-v) = 5; P = u. (-v) = -24 ⇒  S 2   –   4 P   =   5 2   –   4 . ( - 24 )   =   121   >   0

⇒ u và –v là hai nghiệm của phương trình:  x 2   –   5 x   –   24   =   0

Có  Δ   =   ( - 5 ) 2   –   4 . 1 . ( - 24 )   =   121

⇒ Phương trình có hai nghiệm phân biệt

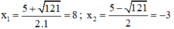
⇒ u = 8; -v = -3 hoặc u = -3; -v = 8

⇒ u = 8; v = 3 hoặc u = -3; v = -8.

- Nếu u + v = -11 và uv = 18 thì u và v là hai nghiệm của phương trình \(x^2+11x+18=0\). Suy ra u = - 2, v = -9 hoặc u = -9; v = -2