(x+1)(x+y)=4 và X^3 + y^3 +12y-14=0
HH
Những câu hỏi liên quan
a) Viết tập hợp X các số tự nhiên x thỏa mãn: x chia hết cho 4 và 2010 x 2025b) Cho y ∈ { 0; 1; 2; 3; 4; 5; 6 }. Thay y bằng chữ số thích hợp để:-
y
12
¯
⋮
3
-
12
y
¯
c
h
i
a
h
ế
t
c
h
o
2
v
à
3
Đọc tiếp
a) Viết tập hợp X các số tự nhiên x thỏa mãn: x chia hết cho 4 và 2010 < x < 2025
b) Cho y ∈ { 0; 1; 2; 3; 4; 5; 6 }. Thay y bằng chữ số thích hợp để:
- y 12 ¯ ⋮ 3
- 12 y ¯ c h i a h ế t c h o 2 v à 3
a) X = {2012 ; 2016 ; 2020 ; 2024}
b)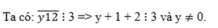
y + 3 ⋮ 3 => y ⋮ 3
Mà: y ∈ {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6} và y ≠ 0 nên y ∈ {3 ; 6}.
Vậy số cần tìm là 312 ; 612.
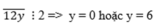
Vậy số cần tìm là 120 ; 126.
Đúng 0
Bình luận (0)
Giải hệ pt
a) \(\left\{{}\begin{matrix}x^2+8y^2=12\\x^3+2xy^2+12y=0\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}x^3+y^3=1\\x^7+y^7=\left(x^4+y^4\right).1\end{matrix}\right.\)
a.
Thay số 12 từ pt trên xuống dưới:
\(x^3+2xy^2+y\left(x^2+8y^2\right)=0\)
\(\Leftrightarrow x^3+x^2y+2xy^2+8y^3=0\)
\(\Leftrightarrow\left(x+2y\right)\left(x^2-xy+4y^2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2y\\x=y=0\left(ktm\right)\end{matrix}\right.\)
Thế vào pt đầu:
\(\left(-2y\right)^2+8y^2=12\Leftrightarrow y^2=1\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=-2\\y=-1\Rightarrow x=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
b.
Thế số 1 từ pt trên xuống dưới:
\(x^7+y^7=\left(x^4+y^4\right)\left(x^3+y^3\right)\)
\(\Leftrightarrow x^4y^3+x^3y^4=0\)
\(\Leftrightarrow x^3y^3\left(x+y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\y=0\\y=-x\end{matrix}\right.\)
Thế vào pt đầu: \(\Rightarrow\left[{}\begin{matrix}y^3=1\\x^3=1\\x^3-x^3=1\left(vô-nghiệm\right)\end{matrix}\right.\)
Vậy nghiệm của hệ là: \(\left(x;y\right)=\left(1;0\right);\left(0;1\right)\)
Đúng 1
Bình luận (0)
Tìm x,y biết :
1. x^2 + y^2 + 2y - 6x + 10 = 0
2. 10- 6x +12y+9x^2 +4y^2 = 0
3. x^2 + 9y^2 + 6y+ 5+4x = 0
4. x^2 + 20 +9y^2 +8x - 12y =0
( Giup mk nha mk đang cần gấp! Thanks mọi người nhiều ! )
1.
\(x^2\)+\(y^2\)+2y-6x+10=0
=> \(x^2\)-6x+9 +\(y^2\)+2y+1=0
=> (x-3)\(^2\)+(y+1)\(^2\)=0
pt vô nghiệm
Đúng 0
Bình luận (1)
4.
=> \(x^2\)+8x+16+(3y)\(^2\)-2.3.2y+4=0
=> (x+4)\(^2\)+(3y-2)\(^2\)=0
pt vô nghiệm
Đúng 0
Bình luận (0)
3.
=> (3y)\(^2\)+2.3y+1+\(x^2\)+4x+4
=> (3y+1)\(^2\)+(x+2)\(^2\)=0
pt vô nghiệm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tim x,y biet:
1)x^2-2x+5+y^2-4y0
2)4x^2+y^2-20x+26-2y0
3)x^2+4y^2+13-6x-8y0
4)4x^2+4x-6y+9x^2+20
5)x^2+y^2+6x-10y+340
6)25x^2-10x+9y^2-12y+50
7)x^2+9y^2-10x-12y+290
89x^2+12x+4y62+8y+80
9)4x^2+9y^2+20x-6y+260
10)3x^2+3y^2+6x-12y+150
11)x^2+4y^2+4x-4y+50
12)4x^2-12x+y^2-4y+130
13)x^2+y^2+2x-6y+100
14)4x^2+9y^2-4x+6y+20
15)y^2+2y+5-12x+9x^20
16)x^2+26+6y+9y^2-10x0
17)10-6x+12y+9x^2+4y^20
18)16x^2+5+8x-4y+y^20
19)x^2+9y^2+4x+6y+50
20)5+9x^2+9y^2+6y-12x0
21)x^2+20+9y62+8x-12y0...
Đọc tiếp
Tim x,y biet:
1)x^2-2x+5+y^2-4y=0
2)4x^2+y^2-20x+26-2y=0
3)x^2+4y^2+13-6x-8y=0
4)4x^2+4x-6y+9x^2+2=0
5)x^2+y^2+6x-10y+34=0
6)25x^2-10x+9y^2-12y+5=0
7)x^2+9y^2-10x-12y+29=0
89x^2+12x+4y62+8y+8=0
9)4x^2+9y^2+20x-6y+26=0
10)3x^2+3y^2+6x-12y+15=0
11)x^2+4y^2+4x-4y+5=0
12)4x^2-12x+y^2-4y+13=0
13)x^2+y^2+2x-6y+10=0
14)4x^2+9y^2-4x+6y+2=0
15)y^2+2y+5-12x+9x^2=0
16)x^2+26+6y+9y^2-10x=0
17)10-6x+12y+9x^2+4y^2=0
18)16x^2+5+8x-4y+y^2=0
19)x^2+9y^2+4x+6y+5=0
20)5+9x^2+9y^2+6y-12x=0
21)x^2+20+9y62+8x-12y=0
22)x^2=4y+4y^2+26-10x=0
23)4y^2+34-10x+12y+x^2=0
24)-10x+y^2-8y+x^2+41=0
25)x^2+9y^2-12y+29-10x=0
26)9x^2+4y^2+4y+5-12x=0
27)4y^2-12x+12y+9x^2=13=0
28)4x^2+25-12x-8y+y^2=0
29)x62+17+4y^2+8x+4y=0
30)4y^2+12y+25+8x+x^2=0
31)x^2+20+9y^2+8x-12y=0
giup mk voi minh can gap ak, cam on cac ban
Giải hệ phương trình: \(\hept{\begin{cases}x^3-x^2+x\left(y^2+1\right)=y^2-y+1\\2y^3+12y^2+18y-2+z=0\\3z^3-9z+x-7=0\end{cases}}\)
Cách giải của bạn Lê Nhật Khôi có phần khồn đúng nhưng nó đã gợi cho mình ý tưởng như này
\(HPT\Leftrightarrow\hept{\begin{cases}\left(1-x\right)\left(x^2+y^2+1\right)=y\\2y\left(y+3\right)^2=2-z\\\left(z-2\right)\left(z+1\right)^2=1-x\end{cases}}\)
\(\Rightarrow-2y\left(y+3\right)^2\left(z+1\right)^2\left(x^2+y^2+1\right)=y\Leftrightarrow y\left[2\left(y+3\right)^2\left(z+1\right)^2\left(x^2+y^2+1\right)+1\right]=0\)
\(\Rightarrow y=0\Rightarrow x=1\Rightarrow\orbr{\begin{cases}z=-1\\z=2\end{cases}}\)
Vũ Đức Minh ok bạn nhá!!!!:)))
Xem thêm câu trả lời
1. 2x(y+1) - 2y(y-1) = 3
và căn(x^2 + y) - x = (4-+y)/2căn(x^2 + y)
2. x + căn(y-1) = 6
và căn(x^2 + 2x +y) + 2x căn(y-1) + 2căn(y-1) = 29
3. 12y/x = 3 + x - 2căn(4y-x)
và căn(y+3) + y = x^2 - x - 3
Mấy bài giải hệ cấp độ cao, nhờ mọi người giải giúp em :)
tự làm đi
Giải hệ phương trình:
\(\hept{\begin{cases}y^3-12y-x^3+6x^2-16=0\\4y^2+2\sqrt{4-y^2}-5\sqrt{4x-x^2}+6=0\end{cases}}\)
Đề bài: Giải hệ phương trình:
\(\left\{{}\begin{matrix}y^3-12y-x^3+6x^2-16=0\left(1\right)\\4y^2+2\sqrt{4-y^2}-5\sqrt{4x-x^2}+6=0\left(2\right)\end{matrix}\right.\).
Giải:
ĐKXĐ: \(\left\{{}\begin{matrix}0\le x\le4\\-2\le y\le2\end{matrix}\right.\).
\(\left(1\right)\Leftrightarrow y^3-12y=\left(x-2\right)^3-12\left(x-2\right)\)
\(\Leftrightarrow\left(x-2-y\right)\left[\left(x-2\right)^2+\left(x-2\right)y+y^2-12\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y+2\\x^2+xy+y^2-4x-2y-8=0\end{matrix}\right.\).
+) TH1: \(x=y+2\): Thay vào (2) ta được:
\(4y^2+2\sqrt{4-y^2}-5\sqrt{4\left(y+2\right)-\left(y+2\right)^2}+6=0\)
\(\Leftrightarrow4y^2+2\sqrt{4-y^2}-5\sqrt{4-y^2}+6=0\)
\(\Leftrightarrow4y^2+6=3\sqrt{4-y^2}\)
\(\Leftrightarrow\left(4y^2+6\right)^2=9\left(4-y^2\right)\)
\(\Leftrightarrow16y^4+57y^2=0\)
\(\Leftrightarrow y=0\Rightarrow x=2\) (TMĐK).
+) TH2: \(x^2+xy+y^2-4x-2y-8=0\):
\(\Leftrightarrow\left(x-2\right)^2+y^2+\left(x-2\right)y=12\).
Do VT \(\le12\) (Đẳng thức xảy ra khi và chỉ khi x = 4; y = 2 hoặc x = 0; y = -2).
Do đó \(\left[{}\begin{matrix}x=4;y=2\\x=0;y=-2\end{matrix}\right.\).
Thử lại không có gt nào thỏa mãn.
Vậy...
Đúng 1
Bình luận (0)
Đường thẳng d song song với hai mặt phẳng (P): 3x + 12y - 3z - 5 0, (Q): 3x - 4y + 9z 0 và đồng thời cắt cả hai đường thẳng
d
1
:
x
+
5
2
y
-
3
-
4
z
+
1...
Đọc tiếp
Đường thẳng d song song với hai mặt phẳng
(P): 3x + 12y - 3z - 5 = 0,
(Q): 3x - 4y + 9z = 0 và đồng thời cắt
cả hai đường thẳng d 1 : x + 5 2 = y - 3 - 4 = z + 1 3 , d 2 : x - 3 - 2 = y + 1 3 = z - 2 4 có phương trình là
![]()
![]()
![]()
![]()
Đáp án D
Cách giải
Vì d song song với hai mặt phẳng (P) và (Q) nên nhận
![]()
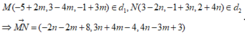

Đúng 0
Bình luận (0)
Đường thẳng d song song với hai mặt phẳng
P
:
3
x
+
12
y
-
3
z
-
5
0
,
Q
:
3
x
-
4
y
+
9
z
+
7
0
và đồng thời cắt cả hai đường thẳng
d
1
:...
Đọc tiếp
Đường thẳng d song song với hai mặt phẳng P : 3 x + 12 y - 3 z - 5 = 0 , Q : 3 x - 4 y + 9 z + 7 = 0 và đồng thời cắt cả hai đường thẳng d 1 : x + 5 2 = y - 3 - 4 = z + 1 3 , d 2 : x - 3 - 2 = y + 1 3 = z - 2 4 có phương trình là
A. x + 3 8 = y + 1 3 = z - 2 4
B. x - 3 8 = y + 1 3 = z - 2 4
C. x + 3 - 8 = y + 1 3 = z + 2 4
D. x + 3 - 8 = y + 1 3 = z - 2 4
Chọn D
Cách giải : Vì d song song với hai mặt phẳng (P) và (Q) nên nhận


Đúng 0
Bình luận (0)


