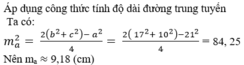Cho tam giác ABC, AB= 17cm, góc C = 62 độ .Tính độ dài đường trung tuyến CM
TT
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB=17cm góc C=62 độ . Tính độ dài đường trung tuyến CM
cho tam giác ABC vuông tại A có AB=17cm,góc C=62 độ tính đường trung tuyến AM
\(sinC=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{sinC}=\dfrac{17}{sin62^0}\approx19,3\left(cm\right)\)
\(AM=\dfrac{1}{2}BC\approx9,65\left(cm\right)\)
Đúng 2
Bình luận (0)
cho tam giác abc cân tại a với đường trung tuyến AH
A/CM TAM GIÁC AHB = TAM GIÁC AHC
B/CM GÓC AHC=GÓC AHB = 90 ĐỘ
C/ Biết AB=AC=13CM,BC=10CM,HÃY TÍNH ĐỘ DÀI ĐƯỜNG TRUNG TUYẾN AH
refer
a) Vì AH là đường trung tuyến của tam giác ABC cân tại A:
nên HB=HC
Xét tam giác AHB và tam giác AHC:
có:+AB=AC( tam giác ABC cân tại A)
+HB=HC(cmt)
+AH: cạnh chung
Vậy tam giác AHB=tam giác AHC(c.c.c)
b) Vì tam giác AHB=tam giác AHC(cmt)
nên: góc AHB=góc AHC=90 độ( 2 góc tương ứng )
c) HB=HC=BC2=102=5cmHB=HC=BC2=102=5cm
Áp dụng định lí Pytago vào tam giác ABH vuông tại H:
có: AB2=AH2+BI2AB2=AH2+BI2
hay:132=AH2+52132=AH2+52
⇒AH2=132−52⇒AH2=132−52
⇔AH=√132−52=12⇔AH=132−52=12
Vậy AH=12cm
Đúng 3
Bình luận (1)
a, Xét Δ AHB và Δ AHC, có :
AH là cạnh chung
AB = AC (Δ ABC cân tại A)
HB = HC (AH là đường trung tuyến của BC)
=> Δ AHB = Δ AHC (c.c.c)
b, Xét Δ ABC cân tại A, có :
AH là đường trung tuyến
=> AH là đường cao
=> \(\widehat{AHC}=\widehat{AHB}=90^o\)
c, đề kì dzậy
Đúng 2
Bình luận (1)
c, Ta có : AH là đường trung tuyến của BC
=> HB = HC
Ta có : BC = HB + HC
=> 10 = HB + HC
=> HB = HC = 10 : 2 = 5 (cm)
Xét Δ AHB vuông tại H, có :
\(AB^2=AH^2+BH^2\) (định lí Py - ta - go)
=> \(13^2=AH^2+5^2\)
=> \(AH^2=144\)
=> AH = 12 (cm)
Đúng 2
Bình luận (1)
1. Cho tam giác ABC có góc B=45 độ, góc C=30 độ , BM là đường trung tuyến của tam giác ABC. Tính số đo góc AMB
2. Cho tam giác ABC có AB=6cm, AC=10cm, độ dài đường trung tuyến AM=4cm. Tính diện tích tam giác ABC
Cho tam giác ABC, biết a = 21cm, b = 17cm, c = 10cm. Tính độ dài đường trung tuyến ma
A. 7,32
B. 8,46
C. 8,94
D. 9,18
cho tam giác ABC cân tại A . vẽ trung tuyến AH
a) CM: tam giác AHB = tam giác AHC
b) CM: góc AHB = goc AHC = 90 độ
c) cho AB=AC=13cm ; BC=10cm,hãy tính độ dài đường trung tuyến AH ?
Cho tam giác ABC có góc A= 120 độ, AB = 4 cm, AC = 6cm. Tính độ dài đường trung tuyến AM
Hạ BD vuông góc với AC tại D; AH vuông góc với BC tại H
 = 120 độ => BÂD = 60 độ.
AB = 4 => AD = 2; BD = 2sqrt3 => CD = 8
Pytago cho tam giác vuông BCD => BC = 2sqrt19.
Tam giác CHA đồng dạng với tam giác CDB (g.g)
=> CH : CD = CA : CB = AH : BD
Thay các số đã biết vào dãy tỉ số trên => CH = 24:(sqrt19); AH = 6(sqrt57) : 19
CM = 1/2BC = sqrt19
=> HM = CH - CM = 5:(sqrt19)
Pytago cho tam giác vuông AHM => AM = ...
Đúng 0
Bình luận (0)
Hạ BD vuông góc với AC tại D; AH vuông góc với BC tại H
 = 120 độ => BÂD = 60 độ.
AB = 4 => AD = 2; BD = 2sqrt3 => CD = 8
Pytago cho tam giác vuông BCD => BC = 2sqrt19.
Tam giác CHA đồng dạng với tam giác CDB (g.g)
=> CH : CD = CA : CB = AH : BD
Thay các số đã biết vào dãy tỉ số trên => CH = 24:(sqrt19); AH = 6(sqrt57) : 19
CM = 1/2BC = sqrt19
=> HM = CH - CM = 5:(sqrt19)
Pytago cho tam giác vuông AHM => AM =
:3
Đúng 0
Bình luận (0)
Bài 1: Cho hình thoi ABCD có cạnh a=30,1975 cm và góc ABC=60 độ . G là trọng tâm tam giác
ABC . Tính diện tích tứ giác AGCD
Bài 2: Cho tam giác ABC vuông tại A có AB=6,251 cm và góc B=56 độ .
a, Tính BC, AC và góc C
b, Tính độ dài đường cao AH và diện tích tam giác ABC
c, Tính độ dài đường trung tuyến AM và phân giác AD của tam giác ABC
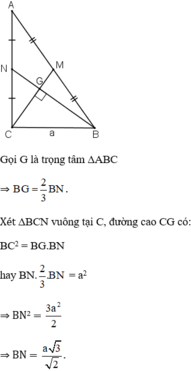
Cho tam giác ABC vuông ở C có đường trung tuyến BN vuông góc với đường trung tuyến CM, cạnh BC = a. Tính độ dài đường trung tuyến BN.