Có bao nhiêu giá trị nguyên dương của m để hpt
 có nghiệ ở nhg cặp số tự nhiên
có nghiệ ở nhg cặp số tự nhiên
GIẢI CHI TIẾT Ạ
\(\left(m^2-2m+1\right)x-4x=-m\)
\(\Leftrightarrow\left(m^2-2m-3\right)x=-m\)
Pt có nghiệm khi \(m\ne\left\{-1;3\right\}\)
Khi đó: \(x=\dfrac{-m}{m^2-2m-3}\)
\(x>0\Rightarrow\dfrac{-m}{m^2-2m-3}>0\)
\(\Rightarrow\left[{}\begin{matrix}m< -1\\0< m< 3\end{matrix}\right.\)
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x - 2 . 12 x + m - 2 9 x có nghiệm dương?
A. 1
B. 2
C. 4
D. 3
( m - 2 ) = 0
m = - 16 x - 2 . 12 x 9 x + 2 = f ( x )
ta dùng mode 7 với
Start 0; end 9; step 0,5 ta nhận thấy f(x) giảm dần và tại x = 0 thì f(x) = 3 nên các giá trị nguyên dương của m để phương trình có nghiệm dương là m = 1; m = 2
Đáp án cần chọn là B
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x - 2 . 12 x + m - 2 . 9 x = 0 có nghiệm dương?
A. 2.
B. 3.
C. 4.
D. 1.
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x − 2.12 x + m − 2 9 x = 0 có nghiệm dương?
A. 1
B. 2
C. 4
D. 3
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x − 2.12 x + m − 2 .9 x = 0 có nghiệm dương?
A. 1
B. 2
C. 4
D. 3
Đáp án B.
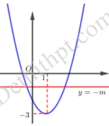
Ta có P T ⇔ 4 3 2 x − 2 4 3 x + m − 2 = 0.
Đặt t = 4 3 x > 0 ⇒ t 2 − 2 t + m − 2 = 0 ⇔ t 2 − 2 t − 2 = − m
Dựa vào đồ thị ta thấy PT có nghiệm lớn hơn 1 ⇔ − m > − 3 ⇔ m < 3
Vậy có 2 giá trị nguyên của m là m = 1 ; m = 2 thỏa mãn yêu cầu bài toán.
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x - 2 . 12 x + m - 2 9 x = 0 có nghiệm dương?
A. 1
B. 2
C. 4
D. 3
Đáp án B.
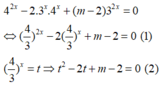
(1) có nghiệm dương ⇔ (2) có nghiệm lớn hơn 1
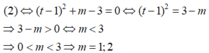
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x - 2 . 12 x + m - 2 . 9 x = 0 có nghiệm dương?
A. 1.
B. 2.
C. 4.
D. 3.
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16x – 2.12x + (m – 2).9x = 0 có nghiệm dương?
A. 1.
B. 2.
C. 4.
D. 3.
Đáp án B.
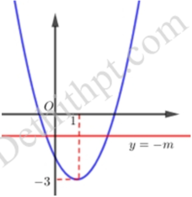
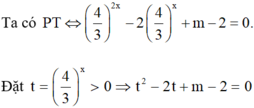
<=> t2 – 2t – 2 = –m
Dựa vào đồ thị ta thấy PT có nghiệm lớn hơn 1 <=> –m > –3 <=> m < 3
Vậy có 2 giá trị nguyên của m là m = l; m = 2 thỏa mãn yêu cầu bài toán.
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16 x - 2 . 12 x + ( m - 2 ) 9 x = 0 có nghiệm dương?
A. 1.
B. 2.
C. 4.
D. 3
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = 3 x 4 - 4 x 3 - 12 x 2 + m có 5 điểm cực trị?
A. 44
B. 27
C. 26
D. 16
Đáp án B
y = 3 x 4 - 4 x 3 - 12 x 2 + m = f x + m , f x = 3 x 4 - 4 x 3 - 12 x 2 f ' x = 12 x 3 - 12 x 2 - 24 x = 12 x x + 1 x - 2 y ' = f ' x f x + m f x + m = 0 ⇒ [ f ' x = 0 f x = - m
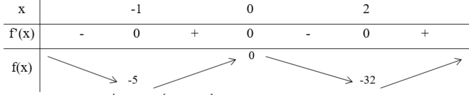 Dựa vào BBT ta thấy hàm số có 5 điểm cực trị khi và chỉ khi
Dựa vào BBT ta thấy hàm số có 5 điểm cực trị khi và chỉ khi
[ - m > 0 - 32 < - m ≤ - 5 ⇒ [ m < 0 5 ≤ m < 32 ⇒ m = 5 ; 6 ; . . . ; 31