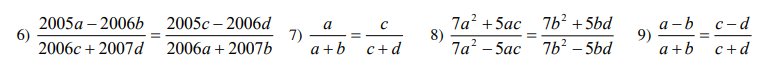
HẾT Ạ
a,2n+9 chia hết cho n+1
b,3n+5 chia hết cho n-1
Giúp mik vs ạ. Đang cần gấp ạ!
a/
\(\dfrac{2n+9}{n+1}=\dfrac{2\left(n+1\right)+7}{n+1}=2+\dfrac{7}{n+1}\)
\(\Rightarrow n+1=\left\{-7;-1;1;7\right\}\Rightarrow n=\left\{-8;-2;0;6\right\}\)
b/
\(\dfrac{3n+5}{n-1}=\dfrac{3\left(n-1\right)+8}{n-1}=3+\dfrac{8}{n-1}\)
\(\Rightarrow n-1=\left\{-8;-4;-2;-1;1;2;4;8\right\}\)
\(\Rightarrow n=\left\{-7;-3;-1;0;2;5;9\right\}\)
Giúp mình vs ạ ko cần giúp hết đâu ạ mình cảm ơn nhìu ạ 
is a big supermarket next to our school
not met him for 3 months
10-day Tet holiday
Cần hết ạ cần gấp c.ơn mn trc ạ
Em cần gấp ạ!!! Bài 6 đến hết ạ

Giúp em lẹ ạ 21h30 hết giờ r ạ
Tìm các số 2 3a b thỏa mãn điều kiện sau : a) Chia hết cho 2 ; 5 và 3 b) Chia hết cho 36
giúp em với ạ! Em cần gấp ạ! Em cảm ơn ạ!
Chỉ cần nói kq thôi à
ok để 23 ab chia hết cho 2 và 5 thì b = 0
để 23a0 chia hết cho 3 thì tổng 2+3+a+0 = 5 + a phải chia hết cho 3
a= 1;4;7
thay vào ta được số 2310; 2340; 2370 .
B đấy mà đọc kĩ đi
giải giúp tớ ạ tớ đang cần gấp mong các ctv giải giúp ạ(hết đề ạ)





 Giải hết và chi tiết với ạ. Em đang cần gấp ạ. Em cảm ơn nhiều ạ.
Giải hết và chi tiết với ạ. Em đang cần gấp ạ. Em cảm ơn nhiều ạ.
Giải giúp mình ạ, làm được bao nhiêu câu cũng được ạ hết thì càng tốt ạ
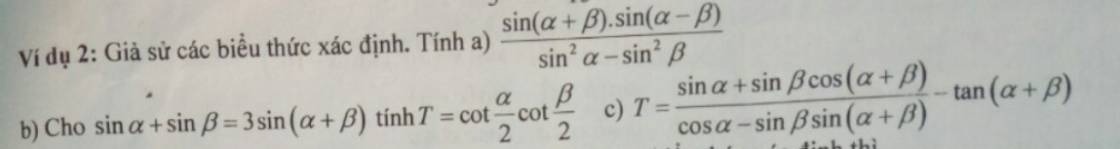
a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)
Mn giải hết giúp em đc ko ạ
Em đang cần gấp ạ
Em cảm ơn nhiều.
Mong mn đừng bơ mà hãy giải hết hộ em .