cho hcn ABCD. Mlaf 1 điểm AD. P,Q là hình chiếu của M trên AB,AD. chứn minh PQ song song BD
LL
Những câu hỏi liên quan
Bài 1: Cho hình thang ABCD (AB//CD); AC giao với BD tại O. Chứn minh rằng OA . OD = OB . OC
Bài 2: Cho hình thang ABCD (AB//CD); một đường thẳng song sonh với AB cắt AD, BC, AC, BD lần lượt tại M, N, P, Q. Chứng minh rằng MN=PQ.
Bài 3: Cho hình thang ABCD (AB//CD); E thuộc BC. Kẻ CK//AE (K thuộc AD). Chứng minh rằng BK//DE.
cho hình chữ nhật ABCD ,M là 1 điểm trên đường chéo AC. Gọi P,Q là thứ tự hình chiếu của M trên AD, AB< chứng minh PQ//BD
Cho hình chữ nhật ABCD (AB > AD). Trên cạnh AD, BC lần lượt lấy các điểm M và N sao cho AM = CN.
d) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. Chứng minh rằng: AC ⊥ CK.
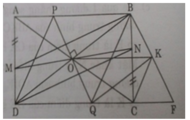
d) Gọi F là giao điểm của BK và QC. Ta có O là trung điểm của BD và OQ // BK (gt) nên Q là trung điểm của DF.
Lại có QK // BD (gt); Q là trung điểm của DF ⇒ K là trung điểm của BF.
CK là trung tuyến của tam giác vuông BCF ⇒ CK = BK = BC/2.
Ta có QK là đường trung bình của tam giác
⇒ QK = BO = BD/2; QK // BO
⇒ Tứ giác OBKQ là hình bình hành
Mặt khác ∠(OBQ) = 90o ⇒ OBKQ là hình chữ nhật
⇒ ∠(OBK) = 90o
Xét ΔOCK và ΔOBK có
CK chung
OC = OB (tính chất đường chéo hình chéo hình chữ nhật)
CK = BK (cmt)
Vậy ΔOCK = ΔOBK (c.c.c) ⇒ ∠OCK = ∠OBK = 90o hay AC ⊥ CK.
Đúng 0
Bình luận (0)
cho hình chữ nhật ABCD. Từ một điểm M trên đường chéo AC vẽ Mp vông góc AB, MQ vông góc AD. Chứng minh PQ song song BD
Xét \(\Delta ABC\) có
\(MP\perp AB;BC\perp AB\)=> MP//BC \(\Rightarrow\frac{AP}{PB}=\frac{AM}{MC}\) (talet trong tam giác)
Xét \(\Delta ADC\)
\(MQ\perp AD;CD\perp AD\)=> MQ//CD \(\Rightarrow\frac{AQ}{QD}=\frac{AM}{MC}\) (talet trong tam giác)
\(\Rightarrow\frac{AP}{PB}=\frac{AQ}{QD}\)
Xét \(\Delta ADB\) có
\(\frac{AP}{PB}=\frac{AQ}{QD}\) => PQ//BD (talet đảo trong tam giác)
Cho HCN ABCD, AB=8cm, BC=6cm. Gọi H là hình chiếu của A trên BD. O là giao điểm 2 đường chéo AC và BD. Qua O kẻ đuồng thẳng song song với AH cắt AD tại E và cắt AB tại I . Cm: IA.BE=IB.AE
Cho hình thang ABCD (AB // CD). Một đường thẳng song song với AB lần lượt cắt các đoạn thẳng AD, BD, AC, BC tại M, N, P, Q.
a/ Chứng minh MN = PQ.
b/ Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD. Chứng minh đường thẳng EF đi qua trung điểm của AB và DC
http://olm.vn/hoi-dap/question/403903.html
Đúng 1
Bình luận (0)
http://olm.vn/hoi-dap/tag/Toan-lop-8.html
Đúng 1
Bình luận (0)
Cho hình thang ABCD (AB // CD). Một đường thẳng song song với AB
lần lượt cắt các đoạn thẳng AD, BD, AC, BC tại M, N, P, Q.
a/ Chứng minh MN = PQ.
b/ Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD.
Mik chỉ cần ý b thôi nhoa
Ý (b) câu hỏi là gì vậy?
Ý b câu hỏi là : Chứng minh EF đi qua trung điểm của AB và CD
Câu (b) không cần dùng M, N, P, Q cho nên mình bỏ chúng đi để đỡ rối mắt.
Gọi X là giao điểm của EF và AB, Y là giao điểm của EF và CD.
- Xét \(\Delta EDY\) có: AX // DY => \(\frac{AX}{DY}=\frac{EX}{EY}\) (hệ quả định lí Ta-lét)
- Xét \(\Delta ECY\) có: BX // CY => \(\frac{BX}{CY}=\frac{EX}{EY}\) (hệ quả định lí Ta-lét)
Từ đó suy ra \(\frac{AX}{DY}=\frac{BX}{CY}\) (1)
- Xét \(\Delta FDY\) có: BX // DY => \(\frac{BX}{DY}=\frac{FX}{FY}\) (hệ quả định lí Ta-lét)
- Xét \(\Delta FCY\) có: AX // CY => \(\frac{AX}{CY}=\frac{FX}{FY}\) (hệ quả định lí Ta-lét)
Từ đó suy ra \(\frac{AX}{CY}=\frac{BX}{DY}\) (2)
Từ (1) và (2) \(\Rightarrow AX=BX,CY=DY\) (vì \(AX,BX,CY,DY>0\))
=> X là trung điểm của AB (đ/n), Y là trung điểm của CD (đ/n)
=> EF đi qua trung điểm của AB và CD (\(X,Y\in EF\)) (đpcm)
cho hình thang ABCD ( AB // CD ). một đường thẳng song song với AB lần lượt cắt các đoạn AD, BD, AC, BC tại M, N, P, Q
a) chứng minh rằng MN = PQ
b) gọi E là giao AD và BC , F là giao của AC và BD . CMR đường thẳng EF đi qua trung điểm AB và DC
Cho hình chữ nhật ABCD (ABAD). Trên cạnh AD,BC lần lượt lấy các điểm M, N sao cho AMCNA) CHỨNG MINH RẰNG BM//DNB) Gọi O là trung điểm của BD. CHỨNG MINH AC, BD, MN đồng quy tại OC) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt CD tại Q. CHỨNG MINH: Tứ giác PBQD là hình thoiD) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. CHỨNG MINH: Tứ giác OBKQ là hình chữ nhật và BC _|_(vuông góc ) OK
Đọc tiếp
Cho hình chữ nhật ABCD (AB>AD). Trên cạnh AD,BC lần lượt lấy các điểm M, N sao cho AM=CN
A) CHỨNG MINH RẰNG BM//DN
B) Gọi O là trung điểm của BD. CHỨNG MINH AC, BD, MN đồng quy tại O
C) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt CD tại Q. CHỨNG MINH: Tứ giác PBQD là hình thoi
D) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. CHỨNG MINH: Tứ giác OBKQ là hình chữ nhật và BC _|_(vuông góc ) OK


