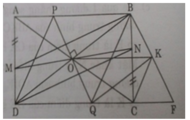
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.c
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.