Trong tình huống nêu ra ở phần mở đầu, viết hệ số phục hồi của quả bóng rổ dưới dạng phân số.
H24
Những câu hỏi liên quan
Chia sẻ cách thể hiện sự tôn trọng và thuyết phục người thân của nhân vật trong tình huống sau:Tình huống: Hưng rất thích chơi bóng rổ và muốn tham gia câu lạc bộ bóng rổ của trường nhưng bố mẹ không đồng ý với lí do gần cuối cấp rồi, nên tập trung vào việc học để năm sau thi chuyển cấp. Sau khi lắng nghe, Hưng lễ phép nói: “Con cảm ơn bố mẹ đã quan tâm và lo lắng cho việc học của con. Nhưng con nghĩ việc tham gia câu lạc bộ bóng rổ của trường sẽ giúp ích cho con về nhiều mặt: Con được giao lưu...
Đọc tiếp
Chia sẻ cách thể hiện sự tôn trọng và thuyết phục người thân của nhân vật trong tình huống sau:
Tình huống: Hưng rất thích chơi bóng rổ và muốn tham gia câu lạc bộ bóng rổ của trường nhưng bố mẹ không đồng ý với lí do gần cuối cấp rồi, nên tập trung vào việc học để năm sau thi chuyển cấp. Sau khi lắng nghe, Hưng lễ phép nói: “Con cảm ơn bố mẹ đã quan tâm và lo lắng cho việc học của con. Nhưng con nghĩ việc tham gia câu lạc bộ bóng rổ của trường sẽ giúp ích cho con về nhiều mặt: Con được giao lưu và học hỏi với các bạn trong câu lạc bộ, rèn được tính kiên trì, cố gắng đạt được mục tiêu, sức khỏe dẻo dai hơn. Hơn nữa, đây cũng là môn thể thao con thíc, nếu được tham gia thì tâm trạng con cũng sẽ phấn chấn hơn, vì thế học tập tốt hơn”

Bạn luôn lễ phép với bố mẹ kể cả khi bố mẹ không đồng ý cho bạn tham gia câu lạc bộ, sau đó bạn đã phân tích, giải thích cho họ những lợi ích của nó và cũng sẽ không ảnh hưởng tới việc học và bạn đã thuyết phục được bố mẹ.
Đúng 1
Bình luận (0)
Hưng nên thẳng thắn nói chuyện với bố mẹ, nên nói rằng là:
"Con đang rất muốn tham gia CLB bóng rổ. Nếu được tham gia thì con sẽ vừa có được đầy đủ sức khỏe, vừa có thể làm được nhiều việc. Và con cũng xin đảm bảo với bố mẹ rằng, cho dù tham gia nhưng con vẫn sẽ đảm bảo việc học để chắc chắn vượt qua kỳ thi chuyển cấp lần này"
Đúng 0
Bình luận (0)
Giáo viên kiểm tra kĩ năng ném bóng vào rổ của một nhóm học sinh và ghi lại kết quả ở bảng dưới đây.a) Hãy nêu số lần ném bóng vào rổ của mỗi bạn. Bạn nào ném bóng vào rổ nhiều nhất? Bạn nào ném bóng vào rổ ít nhất?b) Học sinh có 4 lần ném bóng vào rổ trở lên thì đạt yêu cầu. Vậy trong nhóm học sinh được kiểm tra có bao nhiêu bạn đạt yêu cầu?
Đọc tiếp
Giáo viên kiểm tra kĩ năng ném bóng vào rổ của một nhóm học sinh và ghi lại kết quả ở bảng dưới đây.
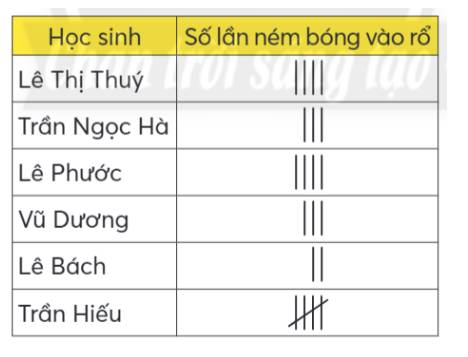
a) Hãy nêu số lần ném bóng vào rổ của mỗi bạn. Bạn nào ném bóng vào rổ nhiều nhất? Bạn nào ném bóng vào rổ ít nhất?
b) Học sinh có 4 lần ném bóng vào rổ trở lên thì đạt yêu cầu. Vậy trong nhóm học sinh được kiểm tra có bao nhiêu bạn đạt yêu cầu?
a) Số lần ném bóng vào rổ của mỗi bạn:
Lê Thị Thúy: 4 lần
Trần Ngọc Hà: 3 lần
Lê Phước: 4 lần
Vũ Dương: 3 lần
Lê Bách: 2 lần
Trần Hiếu: 5 lần
Bạn Trần Hiếu ném bóng vào rổ nhiều nhất, Bạn Lê Bách ném bóng vào rổ ít nhất.
b) Trong nhóm học sinh được kiểm tra có 3 bạn đạt yêu cầu.
Đúng 0
Bình luận (0)
Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hoà loại hai chiều và một chiều mà cửa hàng cần nhập. Từ HĐ1, viết hệ bất phương trình hai ẩn x, y và chỉ ra một nghiệm của hệ này.
- Lập hệ:
Do số lượng máy nhập vào phải là số tự nhiên nên ta có \(x \ge 0,y \ge 0\).
Từ HĐ 1 ta có hai bất phương trình là \(x + y \le 100\) và \(2x + y \le 120\)
Vậy hệ bất phương trình từ HĐ 1 là
\(\left\{ \begin{array}{l}x + y \le 100\\2x + y \le 120\\x \ge 0\\y \ge 0\end{array} \right.\).
Cặp số (x;y)=(50;10) là một nghiệm của hệ BPT vì thay x= 50, y= 10 ta được:
\(\left\{ {\begin{array}{*{20}{l}}
{50 + 10 \le 100}\, \text {(Đúng)}\\
{2.50 + 10 \le 120}\, \text {(Đúng)}\\
{50 \ge 0}\, \text {(Đúng)}\\
{10 \ge 0}\, \text {(Đúng)}
\end{array}} \right.\)
Đúng 0
Bình luận (0)
Có hai thúng đựng đầy quýt như nhau và năm rổ đựng đầy cam như nhau . Số quýt ở mỗi thúng gấp 3 lần ở số cam ở mỗi rổ . Nêu lấy ra ở mỗi thúng 12 quả quýt và ở mỗi rổ 2 quả cam thì số cam còn lại trong các rổ bằng số quýt còn lại trong số quýt còn lại trong các thúng . Hỏi lúc đầu có bao nhiêu quả mỗi loại ?
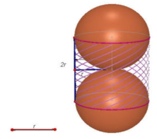
Một cái rổ (trong môn thể thao bóng rổ) dạng một hình trụ đứng, bán kính đường tròn đáy là r (cm), chiều cao 2r (cm), người đặt hai quả bong như hình. Như vậy diện tích toàn bộ của rổ và phần còn lại nhô ra của 2 quả cầu là bao nhiêu. Biết răng mỗi quả bóng bị nhô ra một nửa. A.
4
πr
2
cm
2
B.
6
πr
2
cm
2...
Đọc tiếp
Một cái rổ (trong môn thể thao bóng rổ) dạng một hình trụ đứng, bán kính đường tròn đáy là r (cm), chiều cao 2r (cm), người đặt hai quả bong như hình. Như vậy diện tích toàn bộ của rổ và phần còn lại nhô ra của 2 quả cầu là bao nhiêu. Biết răng mỗi quả bóng bị nhô ra một nửa.
A. 4 πr 2 cm 2
B. 6 πr 2 cm 2
C. 8 πr 2 cm 2
D. 10 πr 2 cm 2
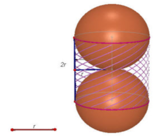
Một cái rổ (trong môn thể thao bóng rổ) dạng một hình trụ đứng, bán kính đường tròn đáy là r (cm), chiều cao 2r (cm), người đặt hai quả bong như hình. Như vậy diện tích toàn bộ của rổ và phần còn lại nhô ra của 2 quả cầu là bao nhiêu. Biết răng mỗi quả bóng bị nhô ra một nửa. A.
4
πr
2
cm
2
B.
6
πr
2
cm
2...
Đọc tiếp
Một cái rổ (trong môn thể thao bóng rổ) dạng một hình trụ đứng, bán kính đường tròn đáy là r (cm), chiều cao 2r (cm), người đặt hai quả bong như hình. Như vậy diện tích toàn bộ của rổ và phần còn lại nhô ra của 2 quả cầu là bao nhiêu. Biết răng mỗi quả bóng bị nhô ra một nửa.
A. 4 πr 2 cm 2
B. 6 πr 2 cm 2
C. 8 πr 2 cm 2
D. 10 πr 2 cm 2
Giải bài toán tình huống mở đầu (kết quả tính theo đơn vị triệu người và làm tròn đến chữ số thập phân thứ hai).
Từ 2020 đến 2050 sẽ là 2050-2020=30(năm)
Dân số VN vào năm 2050 sẽ là:
\(97.34\cdot e^{0.91\%\cdot30}\simeq127,90\)(triệu người)
Đúng 0
Bình luận (0)
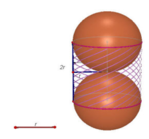
Một cái rổ (trong môn thể thao bong rổ) dạng một hình trụ đứng, bán kính đường tròn đáy là r (cm), chiều cao 2r (cm), người đặt hai quả bong như hình. Như vậy diện tích toàn bộ của rổ và phần còn lại nhô ra của 2 quả cầu là bao nhiêu. Biết răng mỗi quả bóng bị nhô ra một nửa.
Đọc tiếp
Một cái rổ (trong môn thể thao bong rổ) dạng một hình trụ đứng, bán kính đường tròn đáy là r (cm), chiều cao 2r (cm), người đặt hai quả bong như hình. Như vậy diện tích toàn bộ của rổ và phần còn lại nhô ra của 2 quả cầu là bao nhiêu. Biết răng mỗi quả bóng bị nhô ra một nửa.
![]()
![]()
![]()
![]()
Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây ), kể từ khi quả bóng được đá lên; h là độ cao( tính bằng mét ) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở độ cao 6m. Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bó...
Đọc tiếp
Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây ), kể từ khi quả bóng được đá lên; h là độ cao( tính bằng mét ) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở độ cao 6m. Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.
A. y = 4,9 t 2 + 12,2t + 1,2.
B. y = −4,9 t 2 + 12,2t + 1,2.
C. y = −4,9 t 2 + 12,2t − 1,2.
D. y = −4,9 t 2 − 12,2t + 1,2.
Có hai rổ quýt chứa số quýt bằng nhau . Nếu 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở rổ thứ hai bằng một phần ba của bình phương số quả còn lại ở rổ thứ nhất . Hỏi số quả quýt ở mỗi rổ ban đầu là bao nhiêu ?
Pt cần lập là:
X+30 = 1/3(x-30)^2
Giải ta đk: x1=45(tm)
x2=18(ktm)
Đúng 0
Bình luận (0)