Cho hình thang MNPQ (MN//PQ) Gọi I là trung điểm MQ ,IK //MN . Tính độ dài IK biết MN =4cm , PQ=7cm
H24
Những câu hỏi liên quan
Cho hình thang MNPQ (MN//PQ) , I là trung điểm của MQ , K là trung điểm của NP . Biết IK =16,5cm , PQ=18cm . Tính MN?
có:
\(\dfrac{18+MN}{2}=16,5\Leftrightarrow18+MN=33\Leftrightarrow MN=15\)
like cho mk nha
Đúng 0
Bình luận (0)
Cho hình thang MNPQ,MN//PQ.Lấy i là trung điểm MQ .Kẻ iK//MN,K thuộc NP
a.chứng minh rằng :K LÀ TRUNG ĐIỂM NP ?
b.cho MN=5cm,PQ=8cm,tính iK ?
a: Xét hình thang MNPQ có
I là trung điểm của MQ
IK//MN//QP
Do đó: K là trung điểm của NP
b: Xét hình thang MNPQ có
I là trung điểm của MQ
K là trung điểm của NP
Do đó: IK là đường trung bình của hình thang MNPQ
Suy ra: \(IK=\dfrac{MN+PQ}{2}=6.5\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho hình thang MNPQ(MN//PQ),I là trung điểm của MQ,K là trung điểm của NP.Đường thẳng IK cắt NQ ở E,cắt MP ở F.Cho MN=8cm,PQ=12cm.
a)Tính độ IK
b)Chứng minh rằng:IE//MN;FK//MN;IE=FK
a: Xét hình thang MNPQ có
I là trung điểm của MQ
K là trung điểm của NP
Do đó: IK là đường trung bình của hình thang MNPQ
Suy ra: \(IK=\dfrac{MN+QP}{2}=10\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho hình thang MNPQ (MN // PQ). A và B theo thứ tự là trung điểm của MQ và NP. Gọi và K lần lượt là giao điểm của AB với NQ và MP. Biết MN = 8cm và PQ = 16cm a) Chứng minh AI=KB >) Tính AI, KB và IK
a: Xét hình thang MNPQ có
A là trung điểm của MQ
B là trung điểm của NP
Do đó: AB là đường trung bình của hình thang MNPQ
Suy ra: AB//MN//PQ
Xét ΔQMN có AI//MN
nên \(\dfrac{AI}{MN}=\dfrac{AQ}{QM}=\dfrac{1}{2}\left(1\right)\)
Xét ΔPMN có KB//MN
nên \(\dfrac{KB}{MN}=\dfrac{1}{2}\left(2\right)\)
Từ (1) và (2) suy ra AI=KB
Đúng 0
Bình luận (0)
Cho hình thang MNPQ ( MN//PQ, MN,PQ ). Gọi A, B, C, D lần lượt là trung điểm của MN, NP, PQ, QM
1. CMR: tứ giác ABCD là hình bình hành
2. Giả sử MQ vuông góc với NP
a) CMR: tứ giác ABCD là hình chữ nhật
b) Cho MQ= 12cm, NP= 16cm, tính độ dài AC
1: Xét ΔNMP có NA/NM=NB/NP
nên AB//MP và AB=MP/2
Xét ΔQMP có QC/QP=QD/QM
nên DC//MP và DC=MP/2
=>AB//DC và AB=DC
=>ABCD là hình bình hành
Đúng 1
Bình luận (0)
Cho hình thang vuông MNPQ \(\widehat{P}=\widehat{Q}=90^0\), I là trung điểm của MN, \(IK\perp PQ\) . Tính độ dài đoạn QK biết .
Cho hình thang MNPQ , ( MN // PQ ) , MN =m , PQ=n ,qua giao điểm I của 2 đường chéo . Kẻ đường thẳng // với MN cắt MQ , NP theo thứ tự ở H và K . CMR : 1/IH = 1/IK =1/m+1/n
Bài 1: Cho hình thang MNPQ có đáy MN//PQ
a) Cho biết MQ//NP. Chứng minh rằng MN=PQ; MQ=NP
b) Cho biết MN=PQ. Chứng minh rằng MQ//NP; MQ=NP
Bài 2: Cho tứ giác MNPQ có MN=MQ; PN=PQ; góc M=50 độ; góc P=90 độ
a) Tính số đo góc MQN b) Tính số đo góc MQP
c) Chứng minh MP vuông góc với NQ
Các bạn giúp mình nhé. Cảm ơn các bạn.
Bài 1: Cho hình thang MNPQ có đáy MN//PQ
a) Cho biết MQ//NP. Chứng minh rằng MN=PQ; MQ=NP
b) Cho biết MN=PQ. Chứng minh rằng MQ//NP; MQ=NP
Bài 2: Cho tứ giác MNPQ có MN=MQ; PN=PQ; góc M=50 độ; góc P=90 độ
a) Tính số đo góc MQN b) Tính số đo góc MQP
c) Chứng minh MP vuông góc với NQ
Các bạn giúp mình nhé. Cảm ơn các bạn.
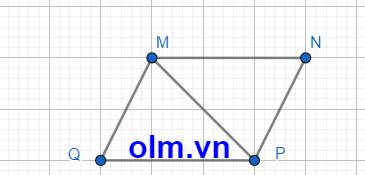
Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
\(\widehat{QPM}\) = \(\widehat{PMN}\) (2 góc so le trong)
\(\widehat{QMP}\) = \(\widehat{NPM}\) (2 góc so le trong)
\(\Rightarrow\) \(\Delta\)MPQ = \(\Delta\)PMN (g-c-g)
\(\Rightarrow\) PQ = MN; MQ = PN (đpcm)
b, Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
MN = PQ
\(\widehat{QPM}\) = \(\widehat{PMN}\) ( 2 góc so le trong)
⇒\(\Delta\)MPQ = \(\Delta\)PMN ( cạnh góc cạnh)
\(\Rightarrow\) MQ = NP (đpcm)
⇒ \(\widehat{QMP}\) = \(\widehat{NPM}\)
Mà hai góc \(\widehat{QMP}\) và \(\widehat{NPM}\) ở vị trí so le trong và bằng nhau nên:
QM // NP (đpcm)
Đúng 2
Bình luận (0)


