tìm tất cả các số tự nhiên sao cho tích (a+1).(b-1)=20. Cảm ơn mọi người ạ
NP
Những câu hỏi liên quan
Tìm tất cả các số tự nhiên a, b sao cho tích (a+1).(b+1)=20
a.b+(1+1)=a.b+2=20:2=10 la b con a = 10-1=9
a=9
b=10
TL :
\(20=1.20=10.2=4.5=5.4=2.10=10.2\)
Ta có bảng sau :
| a + 1 | 1 | 20 | 4 | 5 | 2 | 10 |
| b - 1 | 20 | 1 | 5 | 4 | 10 | 0 |
| a | 0 | 19 | 3 | 4 | 1 | 11 |
| b | 21 | 2 | 6 | 5 | 11 | 3 |
Do ( a + 1 ) . ( b + 1 ) = 20 => a + 1 và b + 1 thuộc Ư(20) = {1;2;4;5;10;20}
Ta có bảng:
| a + 1 | 1 | 2 | 4 | 5 | 10 | 20 |
| a | 0 | 1 | 3 | 4 | 9 | 19 |
| b + 1 | 20 | 10 | 5 | 4 | 2 | 1 |
| b | 19 | 9 | 4 | 3 | 1 | 0 |
Vậy (a,b) thuộc {(0;19);(1;9);(3;4);(4;3);(9;1);(19;0)}
tìm tất cả các số tự nhiên a và b sao cho tích (a+1).(b-1)=20
Vì a+1 nhân b-1 =20 nên a=9 và b=3 vì 9+1=10 ; 3-1=2 ;10 nhân 2 = 20
Đúng 0
Bình luận (0)
Tìm tất cả các số tự nhiên a , k sao cho tích ( a + 1 ) nhân ( b - 1 ) = 20 Giúp Mình Với
a. Tìm số tự nhiên x biết : 12 chia hết cho ( x - 2 )
b. Tìm tất cả các số tự nhiêna , k sao cho tích ( a + 1 ) . (b - 1) = 20
Tìm tất cả số dương a,b,c thoả mãn 1/a + 1/b+1/c=2.
Mọi người giúp tớ với ạ! cảm ơn mọi người nhiều
Số dương? Hay số nguyên dương hả bạn?
Đúng 0
Bình luận (0)
thay các chữ bởi các chữ số thích hợp:
a)a0b = 9ab
b)1abc.5 = abc5
Tất cả đều là số tự nhiên. Kí hiệu nhân là "."
MỌI NGƯỜI GIẢI GIÚP MỀNH NHANH NHẤT CÓ THỂ Ạ. CẢM ƠN!!!
a)Vì a0b=9ab
mà a là chữ số nên a =9
vậy b có thể là các số 0;1;2;3;4;5;6;7;8;9
Đúng 0
Bình luận (0)
Mọi người giúp em 4 bài này với mọi người giải bằng tiếng việt hay là tiếng anh cũng dc ạ (tiếng anh thì tốt ạ)bài 1:Gọi n là số tự nhiên sao cho n + 1 và 2n + 1 đều là số chính phương . Chứng minh rằng n chia hết cho 24.bài2:Tìm tất cả các số tự nhiên n sao cho 2n + 1,3n + 1 đều là bình phương hoàn hảo và 6n + 5 là số nguyên tố.bài3:tìm các số nguyên a, b, c sao cho a^4 + b^4 7c^4 +5.bài4:Tìm tất cả các số nguyên dương x, y và các số nguyên tố p sao cho x^2 −3xy + p^2y^2 12p.
Đọc tiếp
Mọi người giúp em 4 bài này với mọi người giải bằng tiếng việt hay là tiếng anh cũng dc ạ (tiếng anh thì tốt ạ)
bài 1:Gọi n là số tự nhiên sao cho n + 1 và 2n + 1 đều là số chính phương . Chứng minh rằng n chia hết cho 24.
bài2:Tìm tất cả các số tự nhiên n sao cho 2n + 1,3n + 1 đều là bình phương hoàn hảo và 6n + 5 là số nguyên tố.
bài3:tìm các số nguyên a, b, c sao cho a^4 + b^4 = 7c^4 +5.
bài4:Tìm tất cả các số nguyên dương x, y và các số nguyên tố p sao cho x^2 −3xy + p^2y^2 = 12p.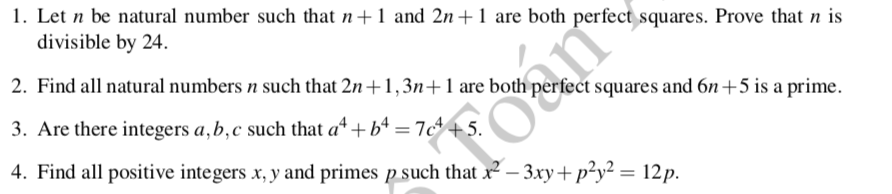
- Chắc là gọi thầy Nguyễn Việt Lâm thôi :)
Đúng 1
Bình luận (2)
1.
\(2n+1\) luôn lẻ \(\Rightarrow2n+1=\left(2a+1\right)^2=4a^2+4a+1\Rightarrow n=2a\left(a+1\right)\)
\(\Rightarrow n\) chẵn \(\Rightarrow n+1\) lẻ \(\Rightarrow\) là số chính phương lẻ
\(\Rightarrow n+1=\left(2b+1\right)^2=4b^2+4b+1\)
\(\Rightarrow n=4b\left(b+1\right)\)
Mà \(b\left(b+1\right)\) là tích 2 số tự nhiên liên tiếp \(\Rightarrow\) luôn chẵn
\(\Rightarrow4b\left(b+1\right)⋮8\Rightarrow n⋮8\)
Mặt khác số chính phương chia 3 chỉ có các số dư 0 và 1
Mà \(\left(n+1\right)+\left(2n+1\right)=3n+2\) chia 3 dư 2
\(\Rightarrow n+1\) và \(2n+1\) đều chia 3 dư 1
\(\Rightarrow n⋮3\)
\(\Rightarrow n⋮24\) do 3 và 8 nguyên tố cùng nhau
Đúng 2
Bình luận (0)
2.
Lý luận tương tự bài 1, ta được n chẵn
Mặt khác các số chính phương chia 5 chỉ có các số dư 0, 1, 4
Mà: \(\left(2n+1\right)+\left(3n+1\right)=5n+2\) chia 5 dư 2
\(\Rightarrow2n+1\) và \(3n+1\) đều chia 5 dư 1
\(\Rightarrow2n⋮5\Rightarrow n⋮5\) (do 2 và 5 nguyên tố cùng nhau)
\(\Rightarrow n=5k\Rightarrow6n+5=5\left(6k+1\right)\)
- TH1: \(k=0\Rightarrow n=0\Rightarrow6n+5\) là SNT (thỏa mãn)
- TH2: \(k>0\Rightarrow6k+1>0\Rightarrow6n+5\) có 2 ước dương lớn hơn 1 \(\Rightarrow\) không là SNT (loại)
Vậy \(n=0\) là giá trị duy nhất thỏa mãn yêu cầu
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
câu 1 : tìm tất cả các số tự nhiên a , b sao cho tích ab=342 và a>b
câu 2 : tìm số tự nhiên có 3 chữ số , biết rằng khi chia số đó cho 17, cho 25 thì được các số dư tương ứng là 8 và 16
Câu 3 : tìm số nguyên tố p sao cho: 5p + 7 là số nguyên tố
Cac bạn giúp mình nhé cảm ơn nhé
Mọi người làm bai ay mình với
Cho hai số tự nhiên a và b. Tìm tất cả các số tự nhiên c sao cho trong ba số, tích của hai số luôn chia hết cho số còn lại.


