Hình bạn tự vẽ nha!!!

a, Vì \(\Delta AOB\) có OA = OB (gt) => \(\Delta AOB\) cân tại O

Xét \(\Delta OAD\) và \(\Delta OBD\)

Có: OA = OB (gt) 

       \(\widehat{AOD}=\widehat{BOD}\) ( gt )

       OD chung

=> \(\Delta OAD=\Delta OBD\left(c.g.c\right)\)

=> DA = DB ( 2 cạnh t/ứng )

b, Xét \(\Delta HOD\) và \(\Delta KOD\)

Có: OD chung 

       \(\widehat{HOD}=\widehat{KOD}\) (gt)

      \(\widehat{DHO}=\widehat{DKO}\left(=90^0\right)\)

=> \(\Delta HOD=\Delta KOD\left(ch.gn\right)\)

=> DH = DK ( 2 cạnh t/ứng )

c, Ta có : \(\widehat{ODA}+\widehat{ODB}=\widehat{ADB}=180^0\) ( 2 góc kề bù )

Vì \(\Delta OAD=\Delta OBD\left(cmt\right)\)

=> \(\widehat{ODA}=\widehat{ODB}\) ( 2 góc t/ứng )

=> \(\widehat{ODA}=\widehat{ODB}=90^0\)

=> \(OD\perp AB\left(đpcm\right)\)

d, Vì \(\Delta ODA=\Delta ODB\left(cma\right)\)

=> AD = BD (2 cạnh t/ứng)

=> D là trung điểm AB

=> AD = BD = AB : 2 = 16 : 2 = 8 cm

Xét \(\Delta ODA\) vuông:

=> OD² + AD² = OA² ( đ/lí Pytago )

Thay số: OD² + 8² = 20²

OD² = 20² - 8²

OD² = 336

=> OD = \(\sqrt{336}\) cm

Vậy...

a, xét tam giác ODA và tam giác ODB có : OD chung

^DOB = ^DOA do OD là pg của ^BOA (gt)

OA = OB (gt)

=> tam giác ODA = tam giác ODB (c-g-c)

b, t đoán đề là cm OD _|_ AB

tam giác ODA = tam giác ODB (câu a)

=> ^ODA = ^ODB (đn)

mà ^ODA + ^ODB = 180 (kb)

=> ^ODA = 90

=> OD _|_ AB

c, xét tam giác BOE và tam giác AOE có : OE chung

^BOD = ^AOD (câu a)

OB = AO (gt)

=> tam giác BOE = tam giác AOE (c-g-c)

=> EB = EA (đn) => E thuộc đường trung trực của AB 

OB = OA (Gt) => O thuộc đường trung trực của AB

=> OE là trung trực của AB

a, xét tam giác AOD và tam giác BOD có:

OA=OB (gt)

góc AOD= góc BOD ( OD là phân giác góc O)

OD chung 

suy ra: tam giác AOD= BOD ( c.g.c)

suy ra: DA=DB (hai cạnh tương ứng)

b, vì tam giác AOD=BOD (chứng minh trên)

suy ra: góc ADO=gócBDO (2 góc tương ứng)

mà góc ADO‹+BDO=180 độ ( kề bù)

suy ra: góc ADO=góc BDO=180/2=90 độ (t/c) 

suy ra: OD vuông góc với AB tại D (t/c)

bài của bạn kacura giống bài bạn bạch cúc bên trên quá há 

mình cx đang ko biết câu đó :)

a, xét tam giác AOD và tam giác BOD có:

OA=OB (gt)

góc AOD= góc BOD ( OD là phân giác góc O)

OD chung 

suy ra: tam giác AOD= BOD ( c.g.c)

suy ra: DA=DB (hai cạnh tương ứng)

b, vì tam giác AOD=BOD (chứng minh trên)

suy ra: góc ADO=gócBDO (2 góc tương ứng)

mà góc ADO‹+BDO=180 độ ( kề bù)

suy ra: góc ADO=góc BDO=180/2=90 độ (t/c) 

suy ra: OD vuông góc với AB tại D (t/c)

Chúc bạn chơi game vui vẻ 🙂 và theo dõi tin tức game trên thegioigame.vn

Không vẽ hình (:

a) Xét tam giác OAD và OAB có :

OA = OB ( gt )

^AOD = ^BOD ( do OD là phân giác của ^O )

OD chung

=> Tam giác OAD = tam giác OAB ( c.g.c )

=> DA = DB ( hai cạnh tương ứng ) ( đpcm )

b) Tam giác OAD = tam giác OBD 

=> ^ODA = ^ODB ( hai góc tương ứng ) ( 1 )

^ODA + ^ODB = 180⁰ ( kề bù ) ( 2 )

Từ ( 1 ) và ( 2 ) => ^ODA = ^ODB = 180⁰/2 = 90

=> OD vuông góc với AB ( đpcm )

\(a,\left\{{}\begin{matrix}OA=OB\\\widehat{AOD}=\widehat{BOD}\left(OD\text{ là p/g}\right)\\OD\text{ chung}\end{matrix}\right.\Rightarrow\Delta OAD=\Delta OBD\left(c.g.c\right)\\ b,\Delta OAD=\Delta OBD\Rightarrow\widehat{ODA}=\widehat{ODB}\\ \text{Mà }\widehat{ODB}+\widehat{ODA}=180^0\\ \Rightarrow\widehat{ODB}=\widehat{ODA}=90^0\\ \Rightarrow OD\bot AB\)

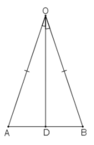
ΔAOD= ΔBOD (chứng minh trên)

⇒ ∠(ADO) = ∠(BDO) (hai góc tương ứng) (1)

Ta có: ∠(ADO) + ∠(BDO) =180o(hai góc kề bù) (2)

Từ (1) và (2) suy ra: ∠(ADO) = ∠(BDO) =90o

Vậy: OD ⊥AB

Đoàn Ngọc Minh Hiếu cóa roảnh

ôg lập lắm nik tek

t vô trag ôg thì ko đăng kí đc TT 

//-_-\\

bó tay 

Ta có hình vẽ

a/ Xét tam giác OAD và tam giác OBD có:

góc AOD = góc BOD (GT)

AD: cạnh chung

OA = OB (GT)

Vậy tam giác OAD = tam giác OBD (c.g.c)

=> DA = DB (2 cạnh tương ứng) (đpcm)

b/ Ta có: tam giác OAD = tam giác OBD (câu a)

=> góc ODA = góc ODB (2 góc tương ứng)

Mà góc ODA + góc ODB = 180⁰ (kề bù)

=> góc ODA = góc ODB = 180⁰ / 2 = 90⁰

Vậy OD \(\perp\) AB (đpcm)