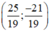giải phương trình bằng phương pháp thế
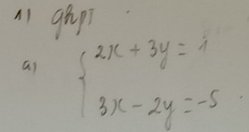
giải hệ phương trình bằng phương pháp thế
\(\left(2\right)\Leftrightarrow\left|x-1\right|=3-3y\)
Thay vào \(\left(1\right)\Leftrightarrow3-3y+\left|y-2\right|=1\Leftrightarrow\left|y-2\right|=3y-2\)
\(\Leftrightarrow\left[{}\begin{matrix}y-2=3y-2\left(y\ge2\right)\\2-y=3y-2\left(y< 2\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=0\left(tkm\right)\\y=1\left(tm\right)\end{matrix}\right.\)
Với \(y=1\Leftrightarrow\left|x-1\right|=3-3=0\Leftrightarrow x=1\)
Vậy \(\left(x;y\right)=\left(1;1\right)\)
giải hệ phương trình sau bằng phương pháp thế
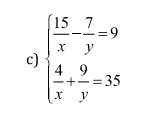
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{135}{x}-\dfrac{63}{y}=81\\\dfrac{28}{x}+\dfrac{63}{y}=245\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{163}{x}=326\\\dfrac{4}{x}+\dfrac{9}{y}=35\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\\dfrac{9}{y}=35-\dfrac{4}{x}=35-8=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{3}\end{matrix}\right.\)
giải hệ phương trình sau bằng phương pháp thế
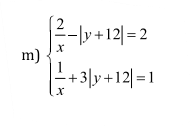
Cho hệ phương trình: 3x-2y=4 (d1)
2x+y=5 (d2)
a) Giải hệ phương trình bằng phương pháp thế?
b) Giải hệ phương trình bằng phương pháp cộng đại số?
c) Vẽ (d1);(d2) trên cùng 1 mặt phẳng toạ độ. Xác định toạ độ giao điểm của d1 và d2
b: \(\left\{{}\begin{matrix}3x-2y=4\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=4\\4x+2y=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=-6\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=5-2x=5-12=-7\end{matrix}\right.\)
Giải hệ phương trình bằng phương pháp thế:
3x + |y| = -1
2x + y = -4
2x+y=-4
\(\Leftrightarrow2x=-4-y\)
\(\Leftrightarrow x=\dfrac{-y-4}{2}\)
Ta có: 3x+|y|=-1
\(\Leftrightarrow\dfrac{-3y-12}{2}+\left|y\right|=-1\)
\(\Leftrightarrow\left|y\right|=\dfrac{-2+3y+12}{2}=\dfrac{3y+10}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{3}{2}y+5\left(y\ge0\right)\\y=-\dfrac{3}{2}y+5\left(y< 0\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\dfrac{-1}{2}y=5\\\dfrac{5}{2}y=5\end{matrix}\right.\Leftrightarrow y\in\varnothing\)
Giải hệ phương trình sau bằng phương pháp thế: 3 x + y = 10 4 x + 5 y = 17
A. (2; 2)
B. (-2; 3)
C. (4; 1)
D. (3; 1)
Đáp án D
Ta có:
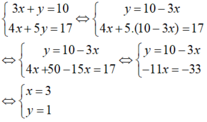
Vậy nghiệm của hệ phương trình đã cho là: (3; 1).
Giải hệ phương trình bằng phương pháp thế.
Giải các hệ phương trình sau bằng phương pháp thế:
7 x - 3 y = 5 4 x + y = 2
7 x - 3 y = 5 1 4 x + y = 2 2
Từ (2) rút ra được y = -4x + 2.
Thế y = -4x + 2 vào phương trình (1) ta được :
7x – 3.(-4x+2) = 5 ⇔ 7x + 12x – 6 = 5 ⇔ 19x = 11 ⇔ 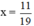
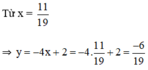
Vậy hệ phương trình có nghiệm duy nhất 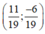
Giải các hệ phương trình sau bằng phương pháp thế: 3 x + 5 y = 1 2 x - y = - 8
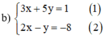
Từ (2) ta rút ra được y = 2x + 8 (*)
Thế (*) vào phương trình (1) ta được :
3x + 5(2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.
Thay x = - 3 vào (*) ta được y = 2.(-3) + 8 = 2.
Vậy hệ phương trình có nghiệm duy nhất (-3 ; 2).
Giải các hệ phương trình sau bằng phương pháp thế: x + 3 y = - 2 5 x - 4 y = 11
x + 3 y = - 2 1 5 x - 4 y = 11 2
Từ (1) rút x theo y ta được: x = -3y – 2
Thế x = -3y – 2 vào phương trình (2) ta được :
5.(-3y – 2) – 4y = 11 ⇔ -15y – 10 – 4y = 11 ⇔ -19y = 21 ⇔ 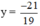
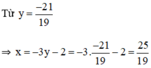
Vậy hệ phương trình có nghiệm duy nhất