Cho tam giác đều ABC nội tiếp (O).Đường cao AH cắt cũng nhỏ BC tại D.Tính số đo góc COD
HH
Những câu hỏi liên quan
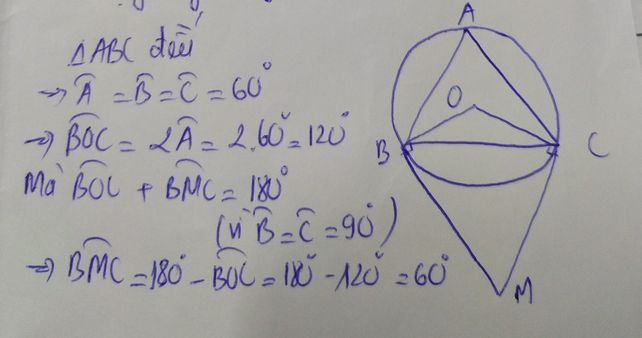
cho tam giác đều ABC nội tiếp (O) . Đường cao AH cắt cung nhỏ BC tại M .Số đo góc BMC =?
cho tam giác ABC cân tại A nội tiếp đường tròn (O), tia AO cắt cung nhỏ BC tại D. Biết số đo cung nhỏ BC bằng 100 độ. Số đo góc COD bằng bao nhiêu?
khi tia OA cắt đường tròn tâm O tại D nên AD là đường kính chia ra 2 cung AD bằng nhau
mà tam giác ABC cân tại A có góc ABC =góc ACB là 2 góc nội tiếp chắc 2 cung AB và AC nên cung AB=cung AC
cung AD=cung AB+cung BD
cung AD=cung AC+cung CD
ta có cung AD=cung AD,cung AB=AC=>cung BD=cung CD
theo đề bài số đo cung nhỏ BD=cung BD+cung CD=>100=2 cung CD=>cung CD bằng 50 độ
MÀ GÓC COD là góc ở tâm chắc cung CD
NÊN SUY RA ĐƯỢC GÓC COD BẰNG 50 ĐỘ
giải thích bạn êy
Cho tam giác ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường tròn ở D. Tính số đo góc ACD
Tam giác ACD nội tiếp trong (O) có AD là đường kính nên suy ra góc CAD = 90 °
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC có 3 góc nhọn, nội tiếp đường tròn (O;R); các đường cao BE,CF cắt nhau tại H. Đường thẳng EF cắt đường tròn ngoại tiếp tam giác ABC tại M,N ( M nằm trên cung nhỏ AB)1) Chứng minh tam giác AMN can2) Giả sử AH cắt BC tại D. Chứng minh rằng: AM^2AH.AD3) Gọi P là điểm đối xứng với A qua O. Đường thẳng PN cắt đường thẳng BC tại K. Chứng minh rằng AK vuông góc với HN.Bài 2: Cho đường tròn tâm O đường kính AB và P là một điểm di động trên đường tròn ( P khác A) sao cho PAle PB.T...
Đọc tiếp
Bài 1: Cho tam giác ABC có 3 góc nhọn, nội tiếp đường tròn (O;R); các đường cao BE,CF cắt nhau tại H. Đường thẳng EF cắt đường tròn ngoại tiếp tam giác ABC tại M,N ( M nằm trên cung nhỏ AB)
1) Chứng minh tam giác AMN can
2) Giả sử AH cắt BC tại D. Chứng minh rằng: \(AM^2=AH.AD\)
3) Gọi P là điểm đối xứng với A qua O. Đường thẳng PN cắt đường thẳng BC tại K. Chứng minh rằng AK vuông góc với HN.
Bài 2: Cho đường tròn tâm O đường kính AB và P là một điểm di động trên đường tròn ( P khác A) sao cho \(PA\le PB\).Trên tia đối PB lấy điểm Q sao cho PQ=PA, dựng hình vuông APQR. Tia PR cắt đường tròn đã cho ở điểm C ( C khác P)
1) Chứng minh C là tâm đường tròn ngoại tiếp tam giác AQB
2) Gọi K là tâm đường tròn nội tiếp tam giác APB, Chứng minh K thuộc đường tròn ngoại tiếp tam giác AQB
3) Kẻ đường cao PH của tam giác APB, gọi \(R_1,R_2,R_3\)lần lượt là bán kính các đường tròn ngoại tiếp tam giác APB, tam giác APH và tam giác BPH.Tìm vị trí điểm P để tổng \(R_1+R_2+R_3\)đạt giá trị lớn nhất
Cho tam giác ABC cân tại A , nội tiếp đường tròn (O) . Đường cao AH cắt đường tròn tại D.
a. cm : AD là đương kính của đường tròn (O)
b. tính số đo góc ACD
c. Cho BC=24cm, AC=20 cm . Tính AH và bán kính đường tròn (O)
Cho tam giác ABC cân tại A , nội tiếp đường tròn (O) . Đường cao AH cắt đường tròn tại D.
a. cm : AD là đương kính của đường tròn (O)
b. tính số đo góc ACD
c. Cho BC=24cm, AC=20 cm . Tính AH và bán kính đường tròn (O)
a. Tam giác ABC cân tại A nên AH là đường cao đồng thời cũng là đường trung trực của BC.
Vì O là tâm của đường tròn ngoại tiếp tam giác ABC nên O nằm trên đường trung trực của BC hay O thuộc AD.
Suy ra AD là đường kính của (O).
b. Tam giác ACD nội tiếp trong (O) có AD là đường kính nên suy ra góc CAD = 90o
c. Ta có :\(AH \perp BC\Rightarrow HB=HC=\frac{BC}{2}=\frac{24}{2}=12\left(cm\right)\)
Áp dụng định lí Pitago vào tam giác vuông ACH ta có:
AC2 = AH2 + HC2
Suy ra: AH2 = AC2 - HC2 = 202 - 122 = 400 - 144 = 256
AH = 16 (cm)
Tam giác ACD vuông tại C nên theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(AC^2=AH.AD\Rightarrow AD=\frac{AC^2}{AH}=\frac{20^2}{16}=25\left(cm\right)\)
Vậy bán kính của đường tròn (O) là: \(R=\frac{AD}{2}=\frac{25}{2}=12,5\left(cm\right)\)
Bán kính đường tron (O) bằng 12,5 cm
Cho đường tròn (O; R), đường kính BC. Lấy điểm A trên đường tròn ( O ) sao cho AB R.a) Tính số đo góc A, góc B, góc C và cạnh AC của tam giác ABC theo Rb)Đường cao AH của tam giác ABC cắt đường tròn ( O ) tại D. Chứng minh: BC là đường trung trực của AD và tam giác ABC đều.c)Tiếp tuyến tại D của đường tròn ( O ) cắt đường thẳng BC tại E. Chứng minh: EA là tiếp tuyến của đường tròn ( O ).d) Chứng minh : EB. CH BH. EC
Đọc tiếp
Cho đường tròn (O; R), đường kính BC. Lấy điểm A trên đường tròn ( O ) sao cho AB = R.
a) Tính số đo góc A, góc B, góc C và cạnh AC của tam giác ABC theo R
b)Đường cao AH của tam giác ABC cắt đường tròn ( O ) tại D. Chứng minh: BC là đường trung trực của AD và tam giác ABC đều.
c)Tiếp tuyến tại D của đường tròn ( O ) cắt đường thẳng BC tại E. Chứng minh: EA là tiếp tuyến của đường tròn ( O ).
d) Chứng minh : EB. CH = BH. EC
Cho đường tròn (O; R), đường kính BC. Lấy điểm A trên đường tròn ( O ) sao cho AB R.a) Tính số đo góc A, góc B, góc C và cạnh AC của tam giác ABC theo Rb)Đường cao AH của tam giác ABC cắt đường tròn ( O ) tại D. Chứng minh: BC là đường trung trực của AD và tam giác ABC đều.c)Tiếp tuyến tại D của đường tròn ( O ) cắt đường thẳng BC tại E. Chứng minh: EA là tiếp tuyến của đường tròn ( O ).d) Chứng minh : EB. CH BH. EC
Đọc tiếp
Cho đường tròn (O; R), đường kính BC. Lấy điểm A trên đường tròn ( O ) sao cho AB = R.
a) Tính số đo góc A, góc B, góc C và cạnh AC của tam giác ABC theo R
b)Đường cao AH của tam giác ABC cắt đường tròn ( O ) tại D. Chứng minh: BC là đường trung trực của AD và tam giác ABC đều.
c)Tiếp tuyến tại D của đường tròn ( O ) cắt đường thẳng BC tại E. Chứng minh: EA là tiếp tuyến của đường tròn ( O ).
d) Chứng minh : EB. CH = BH. EC
Bài 4: Cho (O;R) đường kính BC. Lấy điểm A trên (O) sao cho AB = R
a. Tính số đo các góc A,B,C và cạnh AC theo R
b.Đường cao AH của tam giác ABC cắt (O) tại D. CM: tam giác ADC là tam giác đều
c. Tiếp tuyến tại D của (O) cắt đường thẳng BC tại E.CM EA là tiếp tuyến của (O)
d. CM: EB.CH= BH.EC
Cho tam giác ABC cân tại A, nội tiếp đường tròn(O). Đường cao AH cắt đường tròn ở D.
a, Vì sao AD là đường kính của đường tròn (O).
b, Tính số đo góc ACD
c, Cho BC=24cm,AC=20cm. Tính đường cao AH và bán kính đường tròn (O)
a, Tam giác ABC cân tại A nên AH là đường trung trực của BC. Do đó AD là đường trung trực của BC. Vì O nằm trên đường trung trực của BC nên O nằm trên AD. Vậy AD là đường kính của đường tròn (O).
b, Tam giác ACD nội tiếp đường tròn đường kính AD nên ∠ACD = 90o
c, Ta có BH = HC = BC/2 = 12(cm)
Tam giác AHC vuông tại H nên AH2 = AC2 - HC2 = 202 - 122 = 256
=> AH = 16(cm)
AC2 = AD. AH
AD = AC2/AH = 25(cm)
Bán kính đường tròn(O) bằng 12,5cm.
Đúng 1
Bình luận (0)
a, Tam giác ABC cân tại A nên AH là đường trung trực của BC. Do đó AD là đường trung trực của BC. Vì O nằm trên đường trung trực của BC nên O nằm trên AD. Vậy AD là đường kính của đường tròn (O).
b, Tam giác ACD nội tiếp đường tròn đường kính AD nên ∠ACD = 90o
c, Ta có BH = HC = BC/2 = 12(cm)
Tam giác AHC vuông tại H nên AH2 = AC2 - HC2 = 202 - 122 = 256
=> AH = 16(cm)
AC2 = AD. AH
AD = AC2/AH = 25(cm)
Bán kính 25 cm
Đúng 1
Bình luận (0)