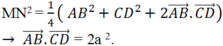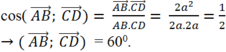cho tứ giác ABCD . gọi M, N lần lượt là trung diểm của AB và CD; E, F, G, H lần lượt là trung điểm của MC, MD, NA, NB. chứng minh 3 đường thẳng EF, GH, MN đồng quy
NU
Những câu hỏi liên quan
cho tứ giác ABCD . gọi M, N lần lượt là trung diểm của AB và CD; E, F, G, H lần lượt là trung điểm của MC, MD, NA, NB. chứng minh 3 đường thẳng EF, GH, MN đồng quy
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Khi đó
M
N
→
bằng: A.
1
2
A
C
→
+
D
B
→
B.
1...
Đọc tiếp
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Khi đó M N → bằng:
A. 1 2 A C → + D B →
B. 1 2 A C → + B D →
C. 1 2 A D → + B C →
D. 1 2 A C → + B D →
Ta có M N → = M A → + A D → + D N → ; M N → = M B → + B C → + C N →
⇒ 2 M N → = M A → + A D → + D N → + M B → + B C → + C N → = ( M A → + M B → ) + ( A D → + B C → ) + ( D N → + C N → ) = 0 → + ( A D → + B C → ) + 0 → = A D → + B C →
⇒ M N → = 1 2 A D → + B C →
Đáp án C
Đúng 0
Bình luận (0)
cho tứ giác abcd gọi m ,n,p,q lần lượt là trung điểm của ab,bc,cd và da chứng minh tứ giác mnpq là hình bình hành
Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔABD
Suy ra: MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình của ΔBCD
Suy ra: NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MQ//NP và MQ=NP
hay MQPN là hình bình hành
Đúng 1
Bình luận (0)
Bài 1. Cho hình bình hành ABCD. Gọi M và N lần lượt là trung điểm của BC và AD. C/m tứ giác BMDN là hình bình hành.
Bài 2. Cho hình bình hành ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Gọi P là giao điểm của DM và AN. Gọi Q là giao điểm của CM và BN. C/m tứ giác PMQN là hình bình hành.
Cho hình bình hành ABCD có CD=2AD;N,M lần lượt là trung diểm các cạnh AB, CD
a) Tứ giác BMDN là hình gì? vì sao ?
b)Gọi giao điểm của BM,DN vs AC lần lượt là H,K. Chứng minh Ch = 1/3 AC
c) Tìm điều kiện của hình bình hành ABCD để BMDN là hình thoi
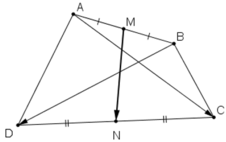
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của DA, BC. Tính góc giữa hai đường thẳng AB và CD biết AB CD 2a;
M
N
a
3
. A. 300 B. 450 C. 600 D. 900
Đọc tiếp
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của DA, BC. Tính góc giữa hai đường thẳng AB và CD biết AB = CD = 2a; M N = a 3 .
A. 300
B. 450
C. 600
D. 900
Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD.
Chứng minh rằng:
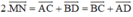
cho tứ giác ABCD . Gọi E,F lần lượt là giao điểm của AB,CD,AD và BC; M,N,P,Q lần lượt là trung điểm của AE,EC,CF,FA. Chứng minh tứ giác MNPQ là hình bình hành
EP // MF (EP là đường trung bình trong ∆BAF) và EP = AF / 2 = MF => MENF là hình bình hành.
=> MP và EF cắt nhau tại trung điểm I.
FN // DE và FN = DE / 2 = QE => FQEN là hình bình hành => QN và EF cắt nhau tại trung điểm I
=> MP và QN cắt nhau tại trung điểm của chúng => MNPQ là hình bình hành
Đúng 1
Bình luận (1)
Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho A M A B = A N A C ; gọi I và J lần lượt là trung điểm của BD, CD. Tứ giác MNJI là hình gì. Tìm điều kiện để tứ giác MNJI là hình bình hành.
+) Vì I, J lần lượt là trung điểm của BD, CD nên IJ là đường trung bình của tam giác BCD. Từ đó suy ra: IJ // BC (3) .
- Từ (1) và (3) suy ra: MN // IJ .
→ Vậy tứ giác MNJI là hình thang.
+) Để MNJI là hình bình hành thì: MI// NJ.
- Lại có ba mặt phẳng (MNJI); (ABD); (ACD) đôi một cắt nhau theo các giao tuyến là MI, NJ, AD nên theo định lý 1 ta có: MI // AD // NJ (4)
- Mà I; J lần lượt là trung điểm BD,CD (5)
- Từ (4)và (5) suy ra: M, N lần lượt là trung điểm của AB, AC.
⇒ Vậy điều kiện để hình thang MNJI trở thành hình bình hành là M, N lần lượt là trung điểm của AB, AC.
Đúng 0
Bình luận (0)