Chơi trò chơi Đôi bàn tay và chiếc mũi kì diệu.
HM
Những câu hỏi liên quan
Chiếc nón kì diệu từng là một trò chơi truyền hình nổi tiếng ở Việt Nam.
Quan sát hình 9.27 và liệt kê tất cả các kết quả có thể khi quay chiếc nón kì diệu.
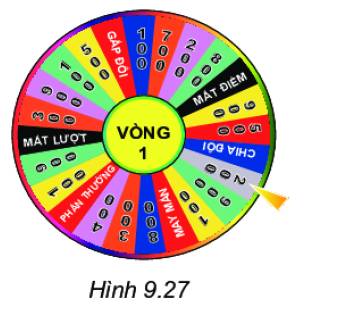
Các kết quả có thể xảy ra là:
100, 700, 200, 800, Mất điểm, 900, 500, Chia đôi, May mắn, 300, 400, Phần thưởng, Mất lượt, Gấp đôi.
Đúng 0
Bình luận (0)
Phần Thưởng, May Mắn,100;700;200;800;Mất điểm;900;500;800;400;300;Mất Lượt, Nhân Đôi
Đúng 0
Bình luận (0)
Có 10 người tham gia đăng kí trò chơi " chiếc nón kì diệu " trên VTV3.Ban tổ chức muốn lấy ra 3 người Hỏi có bao nhiêu cách chọn
không, mình làm sai rồi, kết quả là 120 mới đúng, mình vừa xem lại,
Coi 10 người chơi là 10 số tự nhiên. Ta sẽ lập được 10 x 9 x 7 số có 3 chữ số
(10 cách chọn hàng trăm, mỗi cách chọn hàng trăm có 9 cách chọn hàng chục, mỗi cách chọn hàng chục có 8 cách chọn hàng đơn vị)
Tuy nhiên bài toán này khác với bài toán về lập số có 3 chữ số vì lập số là ta chấp nhận trường hợp đảo vị trí đứng. Trong khi đó cứ mỗi nhóm 3 ta có 6 lần đảo vị trí để được các số khác nhau.
Vậy số cách chọn 3 người chơi là : 10 x 9 x 8 : 6 = 120 (cách)
Đúng 0
Bình luận (0)
Mk k trl nhưng cho mk hỏi nhé
Có phải cậu có bên học 24 đúng k?/?/
Trl câu hỏi thít chó jj ak!!!
Đúng 0
Bình luận (0)
Chiếc kim của bánh xe trong trò chơi “Chiếc nón kì diệu” có thể dừng lại ở một trong 7 vị trí với khả năng như nhau. Xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau bằng A.
5
49
B.
30
49
C.
1
24
D.
1
144
Đọc tiếp
Chiếc kim của bánh xe trong trò chơi “Chiếc nón kì diệu” có thể dừng lại ở một trong 7 vị trí với khả năng như nhau. Xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau bằng
A. 5 49
B. 30 49
C. 1 24
D. 1 144
Chiếc kim của bánh xe trong trò chơi “Chiếc nón kì diệu” có thể dừng lại ở một trong mười vị trí với khả năng như nhau. Xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau là
A. 0,001.
B. 0,72.
C. 0,072.
D. 0,9.
Trong trò chơi “Chiếc nón kì diệu” chiếc kim của bánh xe có thể dừng lại ở một trong 7 vị trí với khả năng như nhau. Tính xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau.
Đọc tiếp
Trong trò chơi “Chiếc nón kì diệu” chiếc kim của bánh xe có thể dừng lại ở một trong 7 vị trí với khả năng như nhau. Tính xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau.
![]()
![]()
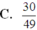
![]()
Đáp án C
Phương pháp: Tính số phần tử của không gian mẫu và số phần tử của biến cố, sau đó suy ra xác suất.
Cách giải: Ba lần quay, mỗi lần chiếc kim có 7 khả năng dừng lại, do đó n Ω = 7 3 = 243
Gọi A là biến cố: “trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau" Khi đó ta có:
Lần quay thứ nhất, chiếc kim có 7 khả năng dừng lại.
Lần quay thứ hai, chiếc kim có 6 khả năng dừng lại.
Lần quay thứ ba, chiếc kim có 5 khả năng dừng lại.
Do đó nA = 7.6.5 = 210
Vậy
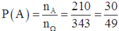
Đúng 0
Bình luận (0)
Trong trò chơi “Chiếc nón kì diệu” chiếc kim của bánh xe có thể dừng lại ở một trong 7 vị trí với khả năng như nhau. Tính xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau.
A
.
3
7
B
.
30
343
C
.
30
49
D
.
...
Đọc tiếp
Trong trò chơi “Chiếc nón kì diệu” chiếc kim của bánh xe có thể dừng lại ở một trong 7 vị trí với khả năng như nhau. Tính xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau.
A . 3 7
B . 30 343
C . 30 49
D . 5 49
Chiếc kim của bánh xe trong trò chơi “ Chiếc nón kì diệu” có thể dừng lại ở một trong mười vị trí với khả năng như nhau. Xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trị khác nhau là A. 0,001 B. 0,72 C. 0,072 D. 0,9
Đọc tiếp
Chiếc kim của bánh xe trong trò chơi “ Chiếc nón kì diệu” có thể dừng lại ở một trong mười vị trí với khả năng như nhau. Xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trị khác nhau là
A. 0,001
B. 0,72
C. 0,072
D. 0,9
Đáp án B
Quay 3 lần thì số kết quả thu được là 103.
Kim của chiếc nón ở 3 vị trí khác nhau ở 3 lần quay có số kết quả là 10.9.8 = 720
Xác suất để kim của chiếc nón ở 3 vị trí khác nhau ở 3 lần quay là 720 10 3 = 18 25 = 0 , 72 .
Đúng 0
Bình luận (0)
Chiếc kim của bánh xe trong trò chơi “ Chiếc nón kì diệu” có thể dừng lại ở một trong mười vị trí với khả năng như nhau. Xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trị khác nhau là A. 0,001 B. 0,72 C. 0,072 D. 0,9
Đọc tiếp
Chiếc kim của bánh xe trong trò chơi “ Chiếc nón kì diệu” có thể dừng lại ở một trong mười vị trí với khả năng như nhau. Xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trị khác nhau là
A. 0,001
B. 0,72
C. 0,072
D. 0,9
Đáp án B
Quay 3 lần thì số kết quả thu được là 10 3 .
Kim của chiếc nón ở 3 vị trí khác nhau ở 3 lần quay có số kết quả là 10.9.8 = 720
Xác suất để kim của chiếc nón ở 3 vị trí khác nhau ở 3 lần quay là : 720 10 3 = 18 25 = 0,72 .
Đúng 0
Bình luận (0)
Chiếc kim của bánh xe trong trò chơi “ Chiếc nón kì diệu” có thể dừng lại ở một trong mười vị trí với khả năng như nhau. Xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trị khác nhau là A. 0,001 B. 0,72 C. 0,072 D. 0,9
Đọc tiếp
Chiếc kim của bánh xe trong trò chơi “ Chiếc nón kì diệu” có thể dừng lại ở một trong mười vị trí với khả năng như nhau. Xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trị khác nhau là
A. 0,001
B. 0,72
C. 0,072
D. 0,9
Đáp án B
Quay 3 lần thì số kết quả thu được là 10 3 .
Kim của chiếc nón ở 3 vị trí khác nhau ở 3 lần quay có số kết quả là 10.9.8 = 720
Xác suất để kim của chiếc nón ở 3 vị trí khác nhau ở 3 lần quay là : 720 10 3 = 18 25 = 0,72
Đúng 0
Bình luận (0)
Chiếc kim của bánh xe trong trò chơi “Chiếc nón kì diệu” có thể dừng lại ở một trong 7 vị trí với khả năng như nhau. Xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau bằng A.
5
49
. B.
30
49
. C.
1
24
. D.
1
144...
Đọc tiếp
Chiếc kim của bánh xe trong trò chơi “Chiếc nón kì diệu” có thể dừng lại ở một trong 7 vị trí với khả năng như nhau. Xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau bằng
A. 5 49 .
B. 30 49 .
C. 1 24 .
D. 1 144 .
Đáp án B
Số phần tử không gian mẫu bằng 7 3 và số kết quả thuận lợi cho biến cố bằng 7.6.5
và xác suất cần tính bằng 7 . 6 . 5 7 3 = 30 49
Đúng 0
Bình luận (0)





