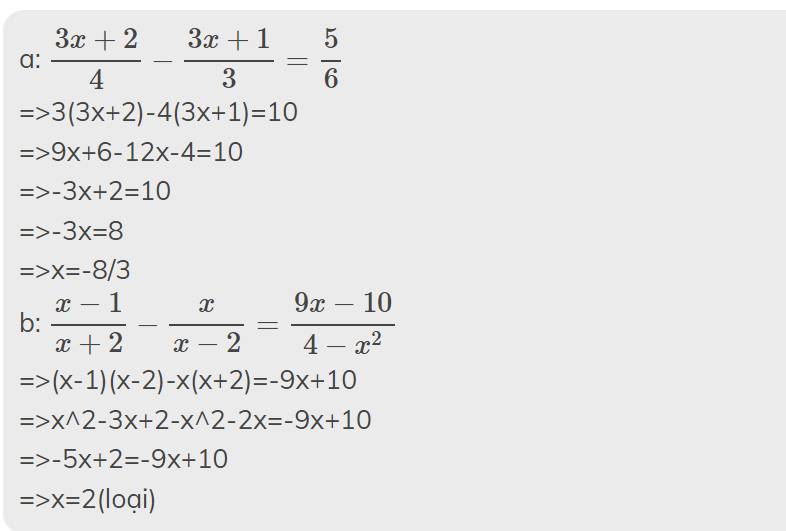ai cho em biết với ạ |3x-1|+4=9 x = bn ạ
CH
Những câu hỏi liên quan
mọi người ơi giúp em với ạ ! giải chi tiết giúp em ạ
1) 3x+2/6- 3x-2/4= 15/8
2) x+2/3+x - x/3-x= 8x-6/9-x ngũ 2
mọi người ơi giúp em với ạ ! giải chi tiết giúp em ạ
1) 3x+2/6- 3x-2/4= 15/8
2) x+2/3+x - x/3-x= 8x-6/9-x ngũ 2
\(1,\dfrac{3x+2}{6}-\dfrac{3x-2}{4}=\dfrac{15}{8}\\ \Leftrightarrow\dfrac{4\left(3x+2\right)}{24}-\dfrac{6\left(3x-2\right)}{24}-\dfrac{45}{24}=0\\ \Leftrightarrow12x+24-18x+12-45=0\\ \Leftrightarrow-6x-9=0\\ \Leftrightarrow x=-\dfrac{3}{2}\)
2, ĐKXĐ:\(x\ne\pm3\)
\(\dfrac{x+2}{3+x}-\dfrac{x}{3-x}=\dfrac{8x-6}{9-x^2}\\ \Leftrightarrow\dfrac{\left(x+2\right)\left(3-x\right)}{\left(3+x\right)\left(3-x\right)}-\dfrac{x\left(3+x\right)}{\left(3+x\right)\left(3-x\right)}-\dfrac{8x-6}{\left(3+x\right)\left(3-x\right)}=0\\ \Leftrightarrow\dfrac{-x^2+x+6-3x-x^2-8x+6}{\left(3+x\right)\left(3-x\right)}=0\\ \Leftrightarrow-2x^2-10x+12=0\\ \Leftrightarrow x^2+5x-6=0\\ \Leftrightarrow\left(x-1\right)\left(x+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-6\left(tm\right)\end{matrix}\right.\)
Đúng 3
Bình luận (1)
\(a,\dfrac{3x+2}{6}-\dfrac{3x-2}{4}=\dfrac{15}{8}\)
\(\Leftrightarrow4\left(3x+2\right)-6\left(3x-2\right)=45\)
\(\Leftrightarrow12x+8-18x+12=45\)
\(\Leftrightarrow12x-18x=45-12-8\)
\(\Leftrightarrow-6x=25\)
\(\Leftrightarrow x=\dfrac{-25}{6}\)
Vậy \(S=\left\{\dfrac{-25}{6}\right\}\)
\(b,\dfrac{x+2}{3+x}-\dfrac{x}{3-x}=\dfrac{8x-6}{9-x^2}\left(ĐKXĐ:x\ne3;x\ne-3\right)\)
\(\Leftrightarrow\left(x+2\right)\left(3-x\right)-x\left(3+x\right)=8x-6\)
\(\Leftrightarrow3x-x^2+6-2x-3x-x^2=8x-6\)
\(\Leftrightarrow-x^2-x^2+3x-2x-3x-8x=-6+6\)
\(\Leftrightarrow-2x^2-10x=0\)
\(\Leftrightarrow-2x\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=5\left(nhận\right)\end{matrix}\right.\)
Vậy \(S=\left\{0;5\right\}\)
Đúng 3
Bình luận (1)
Xét dấu các biểu thức sau
1. f(x) = 3x + 12
2. f(x) = -5x + 9
3. f(x) = -3x - 9
4. f(x) = x(2x+4)
5. f(x) = (x-2) (-x+4)
6. f(x) = (-4x+3) (x-6)
Ai giải hộ em với em cám ơn ạ
1. Ta có : 3x+12=0 <=> x= -4
bảng xét dấu:
| x | -∞ -4 + ∞ |
| 3x+12 |
- 0 + |
f(x) >0 ∀ x ∈ (-4;+∞)
f(x) <0 ∀ x∈ (-∞;-4)
2. Ta có : -5x+9=0 <=> x= \(\frac{9}{5}\)
Bảng xét dấu:
| x | -∞ 9/5 +∞ |
| -5x+9 | + 0 - |
f(x) >0 ∀ x ∈ (-∞; 9/5)
f(x) <0 ∀ x ∈(9/5; +∞)
3. Ta có : -3x-9=0 <=> x= -3
| x | -∞ -3 +∞ |
| -3x-9 | + 0 - |
f(x) >0 ∀ x∈ (-∞; -3)
f(x) <0 ∀x∈ ( -3; +∞ )
4. Ta có : x (2x+4)=0
+, x=0
+, 2x+4=0 <=> x= -2
| x | -∞ -2 0 +∞ |
| x | - \(|\) - 0 + |
| 2x+4 | - 0 + \(|\) + |
| f (x) | + 0 - 0 + |
f(x) >0 ∀ x ∈ (-∞; -2) \(\cup\) (0; +∞)
f(x) <0 ∀ x ∈ (-2;0)
5. Ta có: (x-2)(-x+4)=0
+, x-2=0 <=> x=2
+, -x+4=0 <=> x= 4
| x | -∞ 2 4 +∞ |
| x-2 | - 0 + \(|\) + |
| -x+4 | + \(|\) + 0 - |
| f(x) | - 0 + 0 - |
f(x) >0 ∀ x ∈ (2;4)
f (x) <0 ∀x∈ (-∞;2) \(\cup\)(4; +∞)
6. Ta có : (-4x+3)(x-6)=0
+, -4x+3=0 <=>x= \(\frac{3}{4}\)
+, x-6 =0 <=> x=6
| x | -∞ 3/4 6 +∞ |
| -4x+3 | + 0 - \(|\) - |
| x-6 | - \(|\) - 0 + |
| f(x) | - 0 + 0 - |
f(x) >0 ∀ x∈ (3/4;6)
f(x) <0 ∀ x∈ (-∞; 3/4) \(\cup\)(6;+∞)
Đúng 0
Bình luận (0)
f(x)=(x+2)(3x-9)
f(x) = (6x-4)(2x-3)
f(x)=(1-2x)(-x+4)
Giúp em với ạ. Em đang cần gấp
Tìm x, y biết
(1/3x-5)^2014+(y^4-1/16)8=0
giúp em với ạ!!!
Tìm x, y biết
(1/3x-5)^2014+(y^4-1/16)8=0
giúp em với ạ!!!
Lời giải:
Ta thấy:
$(\frac{1}{3}x-5)^{2014}\geq 0$ với mọi $x$ (do số mũ chẵn)
$(y^4-\frac{1}{16})^8\geq 0$ với mọi $y$
Do đó để tổng của chúng $=0$ thì:
$\frac{1}{3}x-5=y^4-\frac{1}{16}=0$
Có:
$\frac{1}{3}x-5=0$
$\Rightarrow x=15$
$y^4-\frac{1}{16}=0$
$\Rightarrow y^4=\frac{1}{16}=(\frac{1}{2})^4=(\frac{-1}{2})^4$
$\Rightarrow y=\pm \frac{1}{2}$
Đúng 0
Bình luận (0)
(3x-4)^2-9(x-1)(x-3)=13
tl giùm em ạ
Ta có: \(\left(3x-4\right)^2-9\left(x-1\right)\left(x-3\right)=13\)
\(\Leftrightarrow\left(3x-4\right)^2-9\left(x^2-4x+3\right)=13\)
\(\Leftrightarrow9x^2-24x+16-9x^2+36x-27=13\)
\(\Leftrightarrow12x=24\)
hay x=2
Đúng 0
Bình luận (0)
mọi người ơi giúp em với ạ ! em cảm ơn mọi người nhiều lắm ạ !
3x+2/4-3x+1/3=5/6
x-1/x+2-x/x-2=9x-10/4-x ngũ 2
a: \(\dfrac{3x+2}{4}-\dfrac{3x+1}{3}=\dfrac{5}{6}\)
=>3(3x+2)-4(3x+1)=10
=>9x+6-12x-4=10
=>-3x+2=10
=>-3x=8
=>x=-8/3
b: \(\dfrac{x-1}{x+2}-\dfrac{x}{x-2}=\dfrac{9x-10}{4-x^2}\)
=>(x-1)(x-2)-x(x+2)=-9x+10
=>x^2-3x+2-x^2-2x=-9x+10
=>-5x+2=-9x+10
=>x=2(loại)
Đúng 0
Bình luận (0)
1. Tìm x biết:
1. (2-x)^2-9=0
2. (X-3)^3 - (x-3)×(x^2+3x+9)= 15-9(x+1)^2
Mọi người giúp em với ạ, em cảm ơn.
\(1,\left(2-x\right)^2-9=0\)
\(\Leftrightarrow\left(2-x-9\right)\left(2-x+9\right)=0\)
\(\Leftrightarrow\left(-7-x\right)\left(11-x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}-7-x=0\\11-x=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-7\\x=11\end{matrix}\right.\)
\(b,\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)=15-9\left(x+1\right)^2\)\(\Leftrightarrow x^3-9x^2+27x-27-x^3-27=15-9x^2-18x-9\)\(\Leftrightarrow x^3-9x^2+27x-x^3+9x^2+18x=15+27+27\)\(\Leftrightarrow45x=69\Rightarrow x=\dfrac{23}{15}\)
Đúng 0
Bình luận (0)
1. \(\left(2-x\right)^2-9=0\)
\(\left(2-x\right)^2=9\)
\(\left(2-x\right)^2=3^2\)
\(2-x=3\)
\(-x=-1\Rightarrow x=1\)
Đúng 0
Bình luận (0)