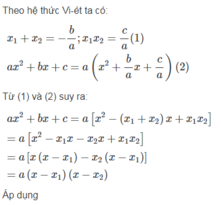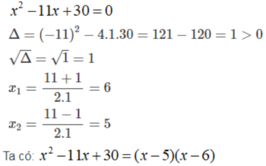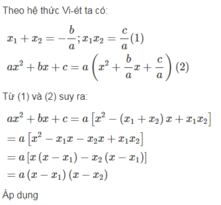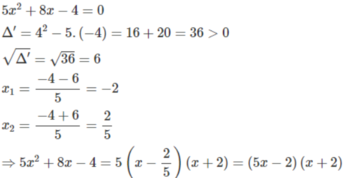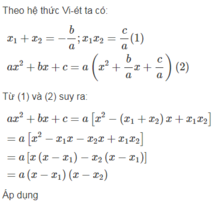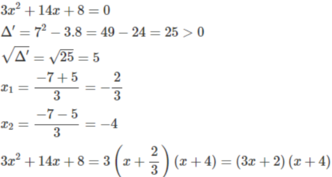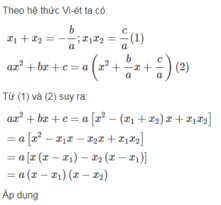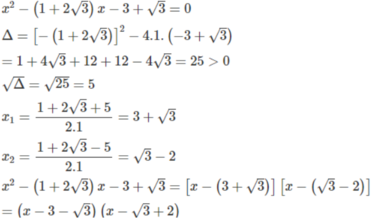phân tích (dạng vi- ét) x2=x13+4x12
HN
Những câu hỏi liên quan
X1^2.x2^2 phân tích ra hệ thức vi ét
X1².X2² = (X1.X2)² = (\(\dfrac{c}{a}\) )2 =\(\dfrac{c^2}{a^2}\)
Hệ thức Vi-ét: X1.X2 = \(\dfrac{c}{a}\)
Đúng 2
Bình luận (0)
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a
x
2
+ bx + c có hai nghiệm
x
1
,
x
2
thì nó phân tích được thành a
x
2
+ bx + c a(x -
x
1
)(x - ...
Đọc tiếp
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a x 2 + bx + c có hai nghiệm x 1 , x 2 thì nó phân tích được thành a x 2 + bx + c = a(x - x 1 )(x - x 2 )
Phân tích các tam thức sau thành tích:
x 2 - 11x + 30
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a
x
2
+ bx + c có hai nghiệm
x
1
,
x
2
thì nó phân tích được thành a
x
2
+ bx + c a(x -
x
1
)(x - ...
Đọc tiếp
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a x 2 + bx + c có hai nghiệm x 1 , x 2 thì nó phân tích được thành a x 2 + bx + c = a(x - x 1 )(x - x 2 )
Phân tích các tam thức sau thành tích:
5 x 2 + 8x - 4
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a
x
2
+ bx + c có hai nghiệm
x
1
,
x
2
thì nó phân tích được thành a
x
2
+ bx + c a(x -
x
1
)(x - ...
Đọc tiếp
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a x 2 + bx + c có hai nghiệm x 1 , x 2 thì nó phân tích được thành a x 2 + bx + c = a(x - x 1 )(x - x 2 )
Phân tích các tam thức sau thành tích:
3 x 2 + 14x + 8
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a
x
2
+ bx + c có hai nghiệm
x
1
,
x
2
thì nó phân tích được thành a
x
2
+ bx + c a(x -
x
1
)(x - ...
Đọc tiếp
Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a x 2 + bx + c có hai nghiệm x 1 , x 2 thì nó phân tích được thành a x 2 + bx + c = a(x - x 1 )(x - x 2 )
Phân tích các tam thức sau thành tích:
5 x 2 - (1 + 2 3 )x - 3 + 3
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 2 x 2 + 9x + 7 = 0
2 x 2 + 9x + 7 = 0
∆ = 9 2 - 4.2.7 = 81 - 56 = 25 > 0
Do đó, phương trình có hai nghiệm phân biệt
Theo hệ thức Vi – et ta có:
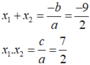
Đúng 0
Bình luận (0)
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 5 x 2 + x + 2 = 0
Ta có: ∆ = 1 2 -4.5.2 = 1 - 40 = -39 < 0
Đúng 0
Bình luận (0)
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 2 x 2 – 7x +2 =0
Ta có: ∆ = - 7 2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x 1 + x 2 =-b/a =7/2 ; x 1 x 2 =c/a =2/2 =1
Đúng 0
Bình luận (0)
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 1,4 x 2 -3x +1,2 =0
Ta có : ∆ = - 3 2 -4.1,4.1,2 =9 – 6,72 =2,28 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x 1 + x 2 = -b/a = 3/(1,4) = 30/14 = 15/7 ; x 1 x 2 = c/a = (1,2)/(1,4) = 12/14 = 6/7
Ta có: Δ = 1 2 -4.5.2 = 1 - 40 = -39 < 0
Đúng 0
Bình luận (0)
x12 + x22 = ?
Vi ét là:
x1 + x2 =7/2
x1.x2= 3
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(\dfrac{7}{2}\right)^2-2.3\)
\(=\dfrac{25}{4}\)
Đúng 2
Bình luận (3)
x1^2+x2^2=(x1+x2)^2-2x1x2
=49/4-2*3=49/4-6
=25/4
Đúng 1
Bình luận (0)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(\dfrac{7}{2}\right)^2-3.2=\dfrac{49}{4}-6=\dfrac{25}{4}\)
Đúng 2
Bình luận (0)