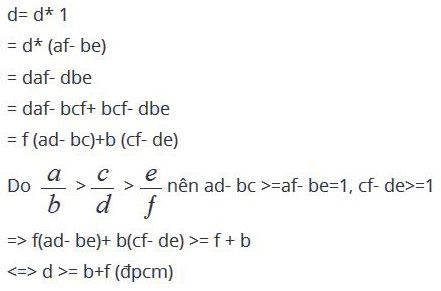cho a,b,c,e,f thuộc Z+ biết a/b>c/d>e/f và af-be=1. Chứng minh d>b+f
LC
Những câu hỏi liên quan
Cho a,b,c,e,f thuộc Z+ biết a/b>c/d>e/f và af-be=1. Chứng minh d>b+f
cho a,b,c,d,e,f thuộc N*
a/b>c/d>e/f và af-be=1. chứng minh rằng d>b+f
cho a,b,c,d,e,f > 0 biết a/b>c/d>e/f và af-be=1.
chứng minh d>=b+f
LÀM GẤP NHA. TIK CHO
cho các số nguyên dương a,b,c,d,e,f sao cho a/b > c/d > e/f. Biết af-be=1. Chứng minh rằng d>b+f
Cho a,b,c,d,e,f thuộc N*; a/b lớn hơn c/d lớn hơn c/f và af...be bằng 1. Chứng minh rằng d lớn hơn b cộng f
Cho số nguyên dương a,b ,c,d,e,f biết \(\frac{a}{b}\)< \(\frac{c}{d}\)<\(\frac{e}{f}\)và af - be = 1
Chứng minh d \(\ge\)b + f
Cho a,b,c,d,e,f nguyên dương thỏa mãn \(\frac{a}{b}>\frac{c}{d}>\frac{e}{f}\) và \(af-be=1\) .Chứng minh:\(d\ge b+f\)
d= d* 1
= d* (af- be)
= daf- dbe
= daf- bcf+ bcf- dbe
= f (ad- bc)+b (cf- de)
Do \(\frac{a}{b}\) >\(\frac{c}{d}\) >\(\frac{e}{f}\)nên ad- bc >=af- be=1, cf- de>=1
=> f(ad- be)+ b(cf- de) >= f + b
<=> d >= b+f (đpcm)
Đúng 0
Bình luận (0)
Cho các số nguyên dương \(a,b,c,d,e,f\) biết :
\(\frac{a}{b}>\frac{c}{d}>\frac{e}{f}\) và \(af-be=1\)
Chứng minh : \(d\ge b+f\)
Lời giải:
Với $a,b,c,d,e,f\in\mathbb{Z}^+$ ta có:
$\frac{a}{b}>\frac{c}{d}\Rightarrow ad>bc\Leftrightarrow ad-bc>0$
Mà $ad,bc$ đều nguyên nên từ đây suy ra $ad-bc\geq 1(*)$
Tương tự:
$\frac{c}{d}>\frac{e}{f}\Rightarrow cf-ed\geq 1(**)$
Từ $(*); (**)$ suy ra:
$d=d(af-be)=daf-dbe=(daf-bcf)+(bcf-dbe)$
$=f(ad-bc)+b(cf-ed)\geq f.1+b.1$
Hay $d\geq b+f$ (đpcm)
Đúng 0
Bình luận (0)
cho các số a, b, c, d,e,f nguyên dương. Biết: (a/f) > (b/d) > (c/e)
và af - be = 1. CMR: d > b + f.
giải giúp với ạ.