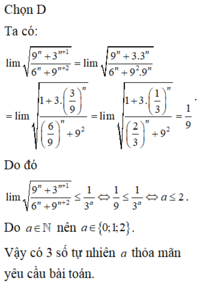Cho n là số tự nhiên chẵn. CMR: A=20n+16n−3n−1A=20n+16n−3n−1 chia hết cho 323
DK
Những câu hỏi liên quan
CMR a, n ³+4n+3 chia hết cho 8 với mọi n là số tự nhiên lẻb, n ³+3n ² - n - 3 chia hết cho 48 với mọi n là số tự nhiên lẻc, n ³( n ²-7) ² -36n chia hết cho 5040 với mọi n là số tự nhiênd, n^4 - 4n ³ - 4n ² +16n chia hết cho 348 với mọi n là số tự nhiên chẵn và n ≥4
Xem chi tiết
a: Với n=3 thì \(n^3+4n+3=3^3+4\cdot3+3=42⋮̸8\) nha bạn
b: Đặt \(A=n^3+3n^2-n-3\)
\(=\left(n^3+3n^2\right)-\left(n+3\right)\)
\(=n^2\left(n+3\right)-\left(n+3\right)\)
\(=\left(n+3\right)\left(n^2-1\right)\)
\(=\left(n-1\right)\left(n+1\right)\left(n+3\right)\)
n lẻ nên n=2k+1
=>\(A=\left(2k+1-1\right)\left(2k+1+1\right)\left(2k+1+3\right)\)
\(=2k\cdot\left(2k+2\right)\left(2k+4\right)\)
\(=8k\left(k+1\right)\left(k+2\right)\)
Vì k;k+1;k+2 là ba số nguyên liên tiếp
nên \(k\left(k+1\right)\left(k+2\right)⋮3!=6\)
=>\(A=8k\left(k+1\right)\left(k+2\right)⋮6\cdot8=48\)
c:


d: Đặt \(B=n^4-4n^3-4n^2+16n\)
\(=\left(n^4-4n^3\right)-\left(4n^2-16n\right)\)
\(=n^3\left(n-4\right)-4n\left(n-4\right)\)
\(=\left(n-4\right)\left(n^3-4n\right)\)
\(=n\left(n-4\right)\left(n^2-4\right)\)
\(=\left(n-4\right)\cdot\left(n-2\right)\cdot n\cdot\left(n+2\right)\)
n chẵn và n>=4 nên n=2k
B=n(n-4)(n-2)(n+2)
\(=2k\left(2k-2\right)\left(2k+2\right)\left(2k-4\right)\)
\(=2k\cdot2\left(k-1\right)\cdot2\left(k+1\right)\cdot2\left(k-2\right)\)
\(=16k\left(k-1\right)\left(k+1\right)\left(k-2\right)\)
Vì k-2;k-1;k;k+1 là bốn số nguyên liên tiếp
nên \(\left(k-2\right)\cdot\left(k-1\right)\cdot k\cdot\left(k+1\right)⋮4!=24\)
=>B chia hết cho \(16\cdot24=384\)
Đúng 1
Bình luận (0)
CMR:
a)n^3+3n^2-n+3 chia hết cho 48 với mọi n lẻ
b)n^4+4n^3-4n^2-16n chia hết cho 384 với mọi n chẵn
1 nếu m, n là các số tự nhiên thỏa mãn 2m^2+m=3n^2+n thì m- n là số nguyên tố
2 chứng minh với n thuộc Z chẵn và n >4 thì n^4-4n^3-16n^2+16 chia hết cho 383
3 cho a, b là số chính phương lẻ. chứng minh (a-1((b-1) chia hết cho 192
4 tìm nghiệm nguyên tố của phương trình x^2- 2y= 1
Tìm số tự nhiên n biết
a) 3n+17 chia hết cho n+2
b) 8n+15 chia hết cho 4n+1
c) 20n+9 chia hết cho 5n-1
d) 3n+11 chia hết cho 2n +3
Các bn giải câu nào cũng đc nha! Càng sớm càng tốt! Tks các bạnn
a. 3n+17= 3(n+2) + 11
3n+17 chia hết cho n+2 khi 11 chia hết cho n+2 suy ra n+2 là ước của 11= (1;11) xét 2 trường hợp
các bài dưới tương tự nhé
Đúng 0
Bình luận (0)
3n+17:(n+2)=3 dư 11
Nếu chia hết thì 11:(n+2), tự giải thích
n+2 là Ư của 11 gồm 1;11;-1;-11
n+2=1=>n=-1
n+2=>11=>n=9
n+2=.-1=>n=-3
n+2=-11=>n=-13
Mình giải hết nghiệm còn n là số tự nhiên nên lấy nghiệm là 9
Đúng 0
Bình luận (0)
b) 8n+15 chia cho 4n+1=2 dư 13 tự chia nha
Chia hết thì 13 chia hết cho 4n+1
Tự giải, tìm n nha bạn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
bài 1: cm
a,n^3+11n chia hết cho 6 vs nEN
b,n^3+17n chia hết cho 6 vs nEN
c,n^3+3n^2-n-3 chia hết cho 48 vs n là số lẻ
d,n^4-4n^3-4n^2+16n chia hết cho 384 vs là số chẵn lớn hơn 4
Tìm số tự nhiên n sao cho 20n-3n chia hết cho n
20n - 3n chia hết cho n ; n ∈ N
17n chia hết cho n
n ∈ Ư (17) = {1; 17}
Vậy n = 1; 17
Có 20n-3n chia hết cho n
=>n(20-3) chia hết cho n
=>n.17 chia hết cho n
Đến đây mk thấy chẳng có lí do gì để n thuộc Ư(17) cả mk ko chắc lắm nhưng đến đó theo mk thì n thuộc mọi số
KB với mk nha
tìm số tự nhiên n để:
a) n^2 + 4n+96 chia hết cho n+1
b)8n^2 + 20n + 50 chia hết cho 2n+3
c)2n^2 + 48 chia hết cho n+ 1
d ) 3n+1 chia hết cho 11-2n
\(a,n^2+4n+96⋮n+1\)
\(\Rightarrow n^2+n+3n+96⋮n+1\)
\(\Rightarrow n\left(n+1\right)+3n+3+93\)
\(\Rightarrow n\left(n+1\right)+3\left(n+1\right)+93⋮n+1\)
\(\Rightarrow\left(n+3\right)\left(n+1\right)+93⋮n+1\)
\(\Rightarrow93⋮n+1\)
=> Tự lập bảng nha OK
Phần b tương tự
Đúng 1
Bình luận (0)
Cho số tự nhiên an=3n2+16n+13(n\(\in N\)).Tìm các số tự nhiên n sao cho an là số chính phương
Có bao nhiêu số tự nhiên a sao cho lim
9
n
+
3
n
+
1
6
n
+
9
n
+...
Đọc tiếp
Có bao nhiêu số tự nhiên a sao cho lim 9 n + 3 n + 1 6 n + 9 n + 2 ≤ 1 3 a ?
A. 1
B. 2019
C. 2
D. 3