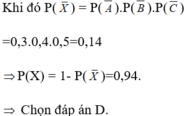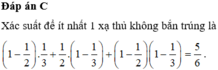Xác suất bắn trúng mục tiêu trong một lần bắn của 3 xạ thủ A,B,C lần lượt là 0,9; 0,8 và 0,7. Tính xác suất sau 3 lượt bắn của mỗi xạ thủ, xạ thủ A bắn trúng mục tiêu nhiều hơn hai xạ thủ còn lại, kết quả làm tròn đến hàng phần triệu
BB
Những câu hỏi liên quan
Hai xạ thủ cùng bắn mỗi nhười một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 1/2 và 1/3
a) Tính xác suất của biến cố X:”cả hai xạ thủ đều bắn trúng bia”
A. 5/6
B. 1/6
C. 2/3
D. 1/3
Gọi A là biến cố “Xạ thủ thứ i bắn trúng bia” i = 1,2.
Khi đó, P(A1) =1/2; P(A2) = 1/3; A1 và A2 độc lập với nhau
X =A1∩ A2 nên P(X) = P(A1∩ A2) = P(A1.A2) = P(A1).P(A2) = 1/6
Chọn đáp án là B
Đúng 0
Bình luận (0)
Hai xạ thủ cùng bắn mỗi nhười một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 1/2 và 1/3
b) Tính xác suất của biến cố Y:”có ít nhất một xạ thủ không bắn trúng bia”
A. 1/2
B. 1/3
C. 1/6
D. 5/6
Gọi A là biến cố “Xạ thủ thứ i bắn trúng bia”, i=1,2
TH1. Xạ thủ thứ nhất bắn trúng, xạ thủ 2 bắn trượt thì xác suất là:
P A 1 = 1 2 . 1 − 1 3
TH2. Xạ thủ thứ nhất bắn trượt, xạ thủ thứ 2 bắn trúng thì xác suất là:
P A 2 = 1 − 1 2 . 1 3
TH3. Cả 2 xạ thủ đều bắn trượt
P A 3 = 1 − 1 2 . 1 − 1 3
Xác suất của biến cố Y là:
P Y = P A 1 + P A 2 + P A 3 = 5 6
Đáp án. D
Đúng 0
Bình luận (0)
Ba người cùng đi săn A, B, C độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A, B, C tương ứng với 0,7; 0,6; 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng? A. 0,75 B. 0,45 C. 0,94 D. 0,80
Đọc tiếp
Ba người cùng đi săn A, B, C độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A, B, C tương ứng với 0,7; 0,6; 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng?
A. 0,75
B. 0,45
C. 0,94
D. 0,80
Đáp án C
Gọi X ¯ là biến cố
Không một xạ thủ nào bắn trúng
![]()
Do A, B, C độc lập với nhau nên A ¯ ; B ¯ ; C ¯ độc lập với nhau
Suy ra P ( X ¯ ) = 0 , 3 . 0 , 4 . 0 , 5 = 0 , 06
![]()
Đúng 0
Bình luận (0)
Ba người cùng đi săn A, B, C độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A, B, C tương ứng với 0,7; 0,6; 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng?
A. 0,75
B. 0,45
C. 0,94
D. 0,80
Đáp án C
Gọi X ¯ là biến cố: Không một xạ thủ nào bắn trúng. Khi đó X ¯ = A ¯ ∪ B ¯ ∪ C ¯ . Do A, B, C độc lập với nhau nên A ¯ ; B ¯ ; C ¯ độc lập với nhau.
Suy ra P X ¯ = 0 , 3 . 0 , 4 . 0 , 5 = 0 , 06 ⇒ P X ¯ = 1 - P X ¯ = 0 , 94 .
Đúng 0
Bình luận (0)
Ba người xạ thủ A1, A2, A3 độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A1, A2, A3 tương ứng là 0,7; 0,6 và 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng. A. 0,45 B. 0,21 C. 0,75 D. 0,94
Đọc tiếp
Ba người xạ thủ A1, A2, A3 độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A1, A2, A3 tương ứng là 0,7; 0,6 và 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng.
A. 0,45
B. 0,21
C. 0,75
D. 0,94
Đáp án D
Gọi X là biến cố: “Không có xạ thủ nào bắn trúng mục tiêu”.
Khi đó P( X ) = P( A ).P( B ).P( C ) = 0,3.0,4.0,5=0,14
=> P(X) = 1- P( X )=0,94.
=> Chọn đáp án D.
Đúng 0
Bình luận (0)
Ba người xạ thủ
A
1
,
A
2
,
A
3
độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của
A
1
,
A
2
,
A
3
tương ứng là 0,7; 0,6 và 0,5. Tính xác suất để có ít nhất mộ...
Đọc tiếp
Ba người xạ thủ A 1 , A 2 , A 3 độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A 1 , A 2 , A 3 tương ứng là 0,7; 0,6 và 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng.
A. 0,45
B. 0,21
C. 0,75
D. 0,94
Hai xạ thủ cùng bắn mỗi người một viên đạn vào bia một cách độc lập. Xác suất bắn trúng bia của hai xạ thủ lần lượt là
1
2
và
1
3
. Xác suất để có ít nhất một xạ thủ không bắn trúng bia bằng A.
1
2
B.
1
6
C.
2
3
D.
5
6
Đọc tiếp
Hai xạ thủ cùng bắn mỗi người một viên đạn vào bia một cách độc lập. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 1 2 và 1 3 . Xác suất để có ít nhất một xạ thủ không bắn trúng bia bằng
A. 1 2
B. 1 6
C. 2 3
D. 5 6
Hai xạ thủ cùng bắn, mỗi người một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là
1
2
và
1
3
. Tính xác suất của biến cố có ít nhất một xạ thủ không bắn trúng bia A.
1
3
B.
1
6
C.
1
2...
Đọc tiếp
Hai xạ thủ cùng bắn, mỗi người một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 1 2 và 1 3 . Tính xác suất của biến cố có ít nhất một xạ thủ không bắn trúng bia
A. 1 3
B. 1 6
C. 1 2
D. 2 3
Đáp án D
Phương pháp:
A, B là các biến cố độc lập thì P ( A . B ) = P ( A ) . P ( B )
Chia bài toán thành các trường hợp:
- Một người bắn trúng và một người bắn không trúng,
- Cả hai người cùng bắn không trúng.
Sau đó áp dụng quy tắc cộng.
Cách giải:
Xác suất để xạ thủ thứ nhất bắn không trúng bia là: 1 − 1 2 = 1 2 .
Xác suất để xạ thủ thứ nhất bắn không trúng bia là: 1 − 1 3 = 2 3 .
Gọi biến cố A:”Có ít nhất một xạ thủ không bắn trúng bia ”.
Khi đó biến cố A có 3 khả năng xảy ra:
+) Xác suất người thứ nhất bắn trúng bia, người thứ hai không bắn trúng bia: 1 2 . 2 3 = 1 3 .
+) Xác suất người thứ nhất không bắn trúng bia, người thứ hai bắn trúng bia: 1 2 . 1 3 = 1 6 .
+) Xác suất cả hai người đều bắn không trúng bia:
Khi đó P ( A ) = 1 2 . 2 3 + 1 2 . 1 3 + 1 2 . 1 3 = 2 3 .
Đúng 0
Bình luận (0)
Hai xạ thủ cùng bắn, mỗi người một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là
1
2
và
1
3
. Tính xác suất của biến cố có ít nhất một xạ thủ không bắn trúng bia.
Đọc tiếp
Hai xạ thủ cùng bắn, mỗi người một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 1 2 và 1 3 . Tính xác suất của biến cố có ít nhất một xạ thủ không bắn trúng bia.
![]()
![]()
![]()
![]()
Đáp án D
Phương pháp:
A, B là các biến cố độc lập thì P(A.B) = P(A).P(B)
Chia bài toán thành các trường hợp:
- Một người bắn trúng và một người bắn không trúng,
- Cả hai người cùng bắn không trúng.
Sau đó áp dụng quy tắc cộng.
Cách giải:
Xác suất để xạ thủ thứ nhất bắn không trúng bia là: 1 - 1 2 = 1 2
Xác suất để xạ thủ thứ nhất bắn không trúng bia là: 1 - 1 3 = 2 3
Gọi biến cố A:”Có ít nhất một xạ thủ không bắn trúng bia ”.
Khi đó biến cố A có 3 khả năng xảy ra:
+) Xác suất người thứ nhất bắn trúng bia, người thứ hai không bắn trúng bia: 1 2 . 2 3 = 1 3
+) Xác suất người thứ nhất không bắn trúng bia, người thứ hai bắn trúng bia: 1 2 . 1 3 = 1 6
+) Xác suất cả hai người đều bắn không trúng bia:
Khi đó
![]()
Đúng 0
Bình luận (0)
Hai xạ thủ cùng bắn, mỗi người một viên đạn vào bia một các độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 12 và 13. Tính xác suất của biến cố có ít nhất một xạ thủ không bắn trúng bia. A.
1
2
B.
1
3
C.
5
6
D.
2
3
Đọc tiếp
Hai xạ thủ cùng bắn, mỗi người một viên đạn vào bia một các độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 12 và 13. Tính xác suất của biến cố có ít nhất một xạ thủ không bắn trúng bia.
A. 1 2
B. 1 3
C. 5 6
D. 2 3