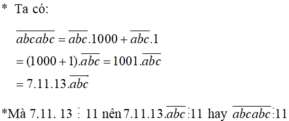Chứng tỏ rằng số có dạng abcabc ( có gạch ngang trên đầu)bao giờ cũng chia hết cho 11
NP
Những câu hỏi liên quan
Chứng tỏ rằng số có dạng abcabc gạch đầu bao giờ cũng chia hết cho 11
Ta có: \(\overline{abcabc}=\overline{abc}.1000+\overline{abc}=\overline{abc}.\left(1000+1\right)\)
\(\Rightarrow\overline{abc}.1001=\overline{abc}.91.11\)
Vì \(11⋮11\Rightarrow\overline{abc}.91.11⋮11\)
Vậy số \(\overline{abcabc}\) lúc nào cũng chia hết cho 11
Đúng 1
Bình luận (0)
abcabc = 1000 . abc + abc = 1001 . abc = 11 . 91 . abc
Vậy abcabc chia hết cho 11.
Đúng 0
Bình luận (2)
ta có abcabc=100000a+10000b+1000b+100a+10b+c
=100100a+10010b+1001c
=1001(100a+10b+c)
=7.143.(100a+10b+c)
=> tích trên có thừa số 7
=> chia hết cho 7
=> abcabc chia hết cho 7
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Chứng tỏ rằng số có dạng (abcabc) bao giờ cũng chia hết cho 11 ( chẳng hạn 328328 ⋮11)
* Chứng tỏ rằng:
a) Số có dạng aaa bao giờ cũng chia hết cho 37.
b) Số có dạng aaaaaa bao giờ cũng chia hết cho 3.
c) Số có dạng abcabc bao giờ cũng chia hết cho 13 và 11.
d) ( ab+ ba) chia hết 11
a ) aaa=a.111=a.(3.37)
=>aaa bao giờ cũng chia hết cho 37
b) aaaaaa=a.111111=a.(3.37037)
=> aaaaaa bao giờ cũng chia hết cho 3
c) abcabc=abc.1001=abc.(7.13.11)
=> abcabc bao giờ cũng chia hết cho 13;11
d) ab+ba=(10a+b)+(10b+a)=(10a+a)+(10b+b)=11a+11b
=> ab+ba chia hết cho 11
ủng hộ nha
Đúng 0
Bình luận (0)
a) aaa = 111a = 37 . 3 . a
b) aaaaaa = 111111a = 37037 . 3 . a
c) abcabc = 1001abc = 77.13 . abc
abcabc = 1001abc = 77.13.abc = 7 .11.13.abc
d) (ab + ba) = 10a + b + 10b + a =11a + 11b = 11.(a+b)
Đúng 0
Bình luận (0)
a) aaa = a x 100 + a x 10 + a =a x 111 =a x 3 x 37 chia hết cho 37
b) aaaaaa = a x 111 111 = a x 3037 x 3 cha hết cho 3
c) abc abc = abc x 1001 = abc x 11 x 13x 7 chia hết cho 11 và 13
d) (ab+ba) = ax10+b + b x10+a=11xa+11xa =11 x(a+b) chia hết cho 11
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11(chẳng hạn: 328328 chia hết cho 11)
abc abc=abc.1000+abc=abc.(1000+1)
=abc.1001=abc.91.11
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11
vậy số abcabc lúc nào cũng chia hết cho 11
Đúng 0
Bình luận (0)
1) Chứng tỏ rằng số có dạng aaa aaa bao giờ cũng chia hết cho 11 (aaa aaa có gạch trên đầu)2) Chứng tỏ rằng số có dạng abc abc bao giờ cũng chia hết cho 11 (abc abc có gạch trên đầu)3) Chứng tỏ rằng lấy một số có hai chữ số, cộng với một số gồm hai chữ số ấy viết theo thứ tự ngược lại, ta luôn luôn được một số chia hết cho 11 (chẳng hạn 37 + 73 110, chia hết cho 11).Giúp mình vs, cần gấp. Bài này là bài 120, 121, 122 trong sách bài tập lớp 6. Không được giải theo sách bài tập nha!
Đọc tiếp
1) Chứng tỏ rằng số có dạng aaa aaa bao giờ cũng chia hết cho 11 (aaa aaa có gạch trên đầu)
2) Chứng tỏ rằng số có dạng abc abc bao giờ cũng chia hết cho 11 (abc abc có gạch trên đầu)
3) Chứng tỏ rằng lấy một số có hai chữ số, cộng với một số gồm hai chữ số ấy viết theo thứ tự ngược lại, ta luôn luôn được một số chia hết cho 11 (chẳng hạn 37 + 73 = 110, chia hết cho 11).
Giúp mình vs, cần gấp. Bài này là bài 120, 121, 122 trong sách bài tập lớp 6. Không được giải theo sách bài tập nha!
\(\overline{aaaa}\) gạch trên đầu bn zô \(fx\) vô hình nì nè 
Đúng 0
Bình luận (2)
Tó biết làm mỗi 2 bài trên thui
1 ) aaa aaa = a . 111 111 = a . 11 . 10101 => chia hết cho 11
2 ) abc abc = abc . 1001 = abc . 11 . 91 = > chia hết cho 11
làm theo cách thầy dạy chứ hoàn toàn ko nhìn sách giải nhé
Đúng 0
Bình luận (2)
Chứng tỏ rằng:
a,Số có dạng aaa (có gạch ngang trên đầu của aaa) luôn chia hết cho 37.
b,Hiệu số: ab - ba ( cả hai đều có gạch ngang ,a nhỏ hơn hoặc bằng b) bao giờ cũng chia hết cho 9.
a) Ta có: aaa=a.111
=a.3.37 chia hết cho 37
b)Ta có: ab-ba=(10a+b)-(10b+a)
=(10a-a)-(10b-b)
=9a-9b
=9(a-b) chia hết cho 9 (đpcm)
Đúng 0
Bình luận (0)
a) Ta có:
aaa = 100a + 10a + a
= 111a
= 3.37.a chia hết cho 37
b) Ta có:
ab - ba = (10a + b) - (10b + a)
= 10a + b - 10b - a
= 9a - 9b
= 9.(a - b) chia hết cho 9
Đúng 0
Bình luận (0)
kb vs mk nha , mk bt cách lm nhứn dài quá , nhác ghi lắm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11(chẳng hạn: 328328 chia hết cho 11)
abc abc=abc.1000+abc=abc.(1000+1)
=abc.1001=abc.91.11
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11
vậy số abcabc lúc nào cũng chia hết cho 11
Đúng 0
Bình luận (0)
ta co abcabc=1000.abc+abc=abc.1001=91.11.abc
ta co 11 chia hết cho 11 nên abcabc chia hêt cho 11
Đúng 0
Bình luận (0)
ta co abcabc = abc . 1001 = 91.11
vì 11 chia hết cho 11 nên abcabc chia hết cho 11
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng tỏ rằng số có dạng aaaaaa gạch trên đầu bao giờ cũng chia hết cho 7
aaaaaa = 111111 . a = 15873 . 7 . a
Vậy aaaaaa chia hết cho 7.
Đúng 0
Bình luận (7)
ta có aaaaaa=100000.a+10000a+1000a+100a+10a+1
=111111a
mà 111111:7=15873
=> aaaaaa:7=15873a
=>aaaaaa chia hết cho 7
Đúng 0
Bình luận (0)
Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11( chẳng hạn 328328 chia hết cho 11 )