Chứng minh rằng: nếu có các số x;y;z;t thõa mãn đẳng thức :[xy(xy-2zt)+z2.t2].[xy(xy-z)-z.(xy+1)]=0
thì nó lập thành 1 tỉ lệ thức
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
1)Cho 7.x+9.x chia hết cho 59 chứng minh 12.x+7.y chia hết cho 59
2)chứng minh rằng nếu abcdef chia hết cho 37 thì số abc+def chia hết cho 37
3)chứng minh rằng nếu số có 6 chữ số abcdef chia hết cho 32 thì 8.(abc+def) chia hết cho 32
ngọc ơi giờ này tao nhớ chúng mày lắm
Chứng minh rằng nếu 1 số có tổng các chữ số bằng 2004 thì số đó là số chính phương
ta có tổng bằng 2011015;\(\sqrt{2011015}\)=1418.102606
Chứng minh rằng hàm số:
f x = x - 1 2 n ế u x ≥ 0 - x 2 n ế u x < 0
Không có đạo hàm tại điểm x = 0 nhưng có đạo hàm tại điểm x = 2 .
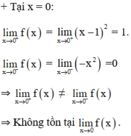
⇒ Không tồn tại đạo hàm của f(x) tại x = 0.
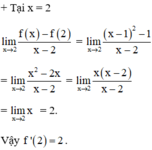
1, Tìm số tự nhiên n để A=(n+5)(n+6) chia hết cho 6n
2, Cho đa thức f(x) = 5x^3+2x^4-x^2+3x^2-x^3-x^4+1-4x^3
Chứng tỏ đa thức trên không có nghiệm
3, Chứng minh rằng nếu x/(a+2b+c) = y/(2a+b-c) = z/(4a-4b+c)
Thì a/(x+2y+z) = b/(2x+y-z) = c/(4x-4y+z)
4, Cho p>3 . Chứng minh rằng nếu các số p, p+d, p+2d là các số nguyên tố thì d chia hết cho 6
5, Chứng minh rằng 5/(1.2.3) + 8/(2.3.4) + 11/(3.4.5) + ..... + 6038/( 2012.2013.2014) <2
Cho x, y là các số thực dương. Chứng minh rằng: nếu x>y thì x^2>y^2 và ngược lại, nếu x^2>y^2 thì x>y
HELP ME!!! LÀM ĐẦY ĐỦ NHA! ĐÚNG CÓ 2 TICK!!
vì x,y là các số dương =>x,y>0
ta có x>y(gt)=>x^2>xy
mà xy >y^2 ( vì x>y) =>x^2>y^2
vì x,y >0 và x^2>y^2 =>căn x^2 > căn y^2 => x>y (đpcm)
Thanks nhé!!
Chứng minh rằng hàm số:
f x = - 2 x nếu x ≥ 0 sin x 2 nếu x < 0
Không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.
Hàm số:
f
x
=
-
2
x
nếu
x
≥
0
sin
x
2
nếu
x
<
0
Không có đạo hàm tại x = 0 vì:
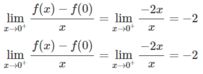
Mặt khác, với x < 0 thì 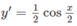
với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
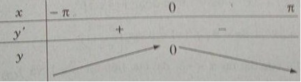
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và y CD = y(0) = 0.
chứng minh rằng nếu một số có tổng các chữ số là 2004 thì số đó không phải là số chính phương
Chứng minh rằng nếu 1 số có tổng các chữ số là 2004 thì số đó không phải là số chính phương
Có tổng các chữ số là 2004, tức số đó chia hết cho 3 và chia 9 dư 2+0+0+4=6, hay không chia hết cho 9 nên không là số chính phương.
Chứng minh rằng nếu một số có tổng các chữ số của nó là 2004 thì số đó là số chính phương
Ta thấy tổng các chữ số của số 2004 là 6 nên 2004 chia hết cho 3
mà không chia hết 9
nên số có tổng các chữ số là 2004 cũng chia hết cho 3 mà không chia hết cho 9,
do đó số này không phải là số chính phương.
Vì số chính phương khi chia cho 3 chỉ có số dư là 0 hoặc 1 . Do tổng các chữ số của số đó là 2004 nên số đó chia hết cho 3. Chứng tỏ số đã cho là số chính phương.
vậy số đã cho có tổng các chưa số là 2004 là một số chính phương
a. Chứng minh rằng nếu mỗi số trong hai số nguyên là tổng các bình phương của hai số nguyên nào đó thì tích của chúng có thể viết dưới dạng tổng hai bình phương.
b. Chứng minh rằng tổng các bình phương của k số nguyên liên tiếp (k = 3, 4, 5) không là số chính phương.