Từ đỉnh A và C của hình bình hành ABCD( AB#BC) và góc B tù. Kẻ các đg vuông góc AM và Cn tới đg thẳng BD.C/m răng tứ giác AMCN là hình bình hành
DT
Những câu hỏi liên quan
Cho hình bình hành abcd trên cạnh AB lấy 3 điểm phân biệt trên cạnh CD lấy 5 điểm phân biệt Hỏi có bao nhiêu tam giác mà các đỉnh của nó được lấy từ đỉnh của hình bình hành và 8 điểm nói trên
Trong mặt phẳng Oxy cho hình bình hành ABCD với A(2;4), B(-3;1), C(3;-1) và D(8;2).
a/ Tính tọa độ chân A' của đường cao vẽ từ đỉnh A của tam giác ABC
b/ Tính diện tích của hình bình hành ABCD
vì trên diễn đàn này toàn câu hỏi hồi rác
ok bạn thực ra mình cũng chang cần k đâu.
nhung mat cong tra loi cho mot nguoi hoi linh tinh that chan
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có diện tích là 36cm2. Tính chu vi của hình bình hành đó biết chiều cao hạ từ đỉnh A vuông góc với cạnh DC là 3cm và bằng ![]() 1/2 chiều cao hạ từ đỉnh D vuông góc với cạnh AD?
1/2 chiều cao hạ từ đỉnh D vuông góc với cạnh AD?
Cho hình chữ nhật ABCD có chiều dài 12 cm, chiều rộng 5 cm. Nối đỉnh A với trung điểm N của cạnh DC. Nối đỉnh C với trung điểm M của cạnh AB. Cho biết hình tứ giác AMCN là hình bình hành có chiều cao MN bằng chiều rộng của hình chữ nhật.a) Giải thích tại sao AN và Mc song song và bằng nhau.b) Diện tích hình chữ nhật ABCD gấp mấy lần diện tích hình bình hành AMCN?
Đọc tiếp
Cho hình chữ nhật ABCD có chiều dài 12 cm, chiều rộng 5 cm. Nối đỉnh A với trung điểm N của cạnh DC. Nối đỉnh C với trung điểm M của cạnh AB. Cho biết hình tứ giác AMCN là hình bình hành có chiều cao MN bằng chiều rộng của hình chữ nhật.
a) Giải thích tại sao AN và Mc song song và bằng nhau.
b) Diện tích hình chữ nhật ABCD gấp mấy lần diện tích hình bình hành AMCN?
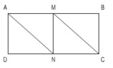
a) Hai đoạn thẳng AN và MC song song và bằng nhau vì chúng là hai cạnh đối diện của hình bình hành AMCN.
b) Diện tích hình chữ nhật ABCD là:
12 × 5 = 60 ( c m 2 )
Vì N là trung điểm của DC nên NC dài :
12 ∶ 6 = 6 cm
Diện tích hình bình hành AMCN là :
6 × 5 = 30( c m 2 )
So với diện tích hình bình hành AMCN thì diện tích hình chữ nhật ABCD gấp: 60 : 20 = 2 lần
Nói thêm : Có thể giải câu b gấp đôi đồ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD gắp đôi bộ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD bằng chiều cao hình bình hành.
Vậy diện tích hình chữ nhật gập đôi diện tích hình bình hành.
Cách 3 :
Đường gấp khúc AMNC chia hình chữ nhật ABCD thành 4 tam giác (vuông) bằng nhau. Hình bình hành AMNC gồm 2 tam giác ấy. Vậy diện tích hình chữ nhật ABCD gấp đôi diện tích hình bình hành AMCN.
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có chiều dài 12 cm, chiều rộng 5 cm. Nối đỉnh A với trung điểm N của cạnh DC. Nối đỉnh C với trung điểm M của cạnh AB. Cho biết hình tứ giác AMCN là hình bình hành có chiều cao MN bằng chiều rộng của hình chữ nhật.a) Giải thích tại sao AN và Mc song song và bằng nhau.b) Diện tích hình chữ nhật ABCD gấp mấy lần diện tích hình bình hành AMCN ?
Đọc tiếp
Cho hình chữ nhật ABCD có chiều dài 12 cm, chiều rộng 5 cm. Nối đỉnh A với trung điểm N của cạnh DC. Nối đỉnh C với trung điểm M của cạnh AB. Cho biết hình tứ giác AMCN là hình bình hành có chiều cao MN bằng chiều rộng của hình chữ nhật.
a) Giải thích tại sao AN và Mc song song và bằng nhau.
b) Diện tích hình chữ nhật ABCD gấp mấy lần diện tích hình bình hành AMCN ?
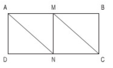
a) Hai đoạn thẳng AN và MC song song và bằng nhau vì chúng là hai cạnh đối diện của hình bình hành AMCN.
b) Diện tích hình chữ nhật ABCD là:
12 × 5 = 60 (cm2)
Vì N là trung điểm của DC nên NC dài :
12 ∶ 2 = 6 cm
Diện tích hình bình hành AMCN là :
6 × 5 = 30(cm2)
So với diện tích hình bình hành AMCN thì diện tích hình chữ nhật ABCD gấp : 60 : 20 = 2 lần
Nói thêm : Có thể giải câu b gấp đôi đồ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD gắp đôi bộ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD bằng chiều cao hình bình hành.
Vậy diện tích hình chữ nhật gập đôi diện tích hình bình hành.
Cách 3 :
Đường gấp khúc AMNC chia hình chữ nhật ABCD thành 4 tam giác ( vuông) bằng nhau. Hình bình hành AMNC gồm 2 tam giác ấy. Vậy diện tích hình chữ nhật ABCD gấp đôi diện tích hình bình hành AMCN.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có chiều dài cạnh CD = 8cn , cạnh bên AD = 6 cm và chiều cao nối từ đỉnh A xuống cạnh CD dài 5cm. Tính chu vi, diện tích của hình bình hành ABCD?
Cho hình chữ nhật ABCD có chiều dài 12cm, chiều rộng 5cm. Nối đỉnh A với trung điểm N của cạnh DC. Nối đỉnh C với trung điểm M của cạnh AB. Cho biết hình tứ giác AMCN là hình bình hành có chiều cao MN bằng chiều rộng của hình chữ nhật.a] Giải thích tại sao đoạn thẳng AN và MC song song và bằng nhau.b] Diện tích hình chữ nhật ABCD gấp mấy lần diện tích hình bình hành AMCN ?
Đọc tiếp
Cho hình chữ nhật ABCD có chiều dài 12cm, chiều rộng 5cm. Nối đỉnh A với trung điểm N của cạnh DC. Nối đỉnh C với trung điểm M của cạnh AB. Cho biết hình tứ giác AMCN là hình bình hành có chiều cao MN bằng chiều rộng của hình chữ nhật.
a] Giải thích tại sao đoạn thẳng AN và MC song song và bằng nhau.
b] Diện tích hình chữ nhật ABCD gấp mấy lần diện tích hình bình hành AMCN ?
diện tích hình CN là 60 xăng ti mét vuông diện tích hình bình hành là 30 xăng ti mét vuông và gấp 2 lần
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A,C xuống BD. Chứng minh AHCK là hình bình hành
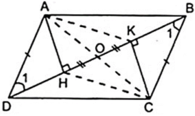
Từ giả thiết ta có:
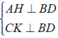
⇒ AH//CK. ( 1 )
Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:
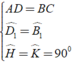
⇒ Δ ADH = Δ CBK
(trường hợp cạnh huyền – góc nhọn)
⇒ AH = CK (cạnh tương tứng bằng nhau) ( 2 )
Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD. Lấy điểm M trên BC và điểm N trên AB sao cho AM = CN. Chứng minh rằng SDAM = SDNC từ đó suy ra đỉnh D của hình bình hành cách đều hai đường thẳng AM, CN

