tìm x
a, x.y=20 và x<y b x.(x+1)=30
Tìm hai số tự nhiên x, y biết
a) x+y=20 và ƯCLN (x,y)=5
b) x+y=240 và ƯCLN (x,y)=40
c) x.y=6 và ƯCLN (x,y)=1
d) x.y=240 và ƯCLN (x,y)=20
a, Do UCLN là 5 nên a, b chia hết cho 5 => tận cùng là 0 hoặc 5
Ta có 20 = 15 + 5 = 18 + 2=19+1=17+3=16+4=14+6=13+7=12+8=11+9
=> 2 số a và b là 15 và 5 hoặc 5 và 15
Bài sau làm tương tự em nhé :)
Tìm tập hợp các số nguyên x biết :
| x + 1 | < 2
Tìm tập hợp các số nguyên x biết :
| x + 1 | < 2
2 SỐ x và y thuộc N biết x.y=420 và ƯCLN( x,y)=20. tìm x và y
Tìm hai số x,y ∈ N* biết rằng x.y = 20 và BCNN(x,y) = 10
- Đặt (x; y) = d nên x = d.m; y = d.n với (m;n) =1. Giả sử x ≤ y thì m ≤ n.
- Ta có: x.y = dm.dn= d2.mn
BCNN(x; y) = x y x ; y = d 2 m . n d = d . m . n
- Ta có: BCNN (x;y) = 10 và x. y = 20 nên d = x y B C N N ( x ; y ) = 20 10 = 2
=> 2.m.n =10 nên m.n = 5
Bảng giá trị
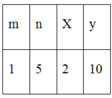
Tìm hai số x,y thuộc N* , biết rằng x.y = 20 và BCNN(x,y) = 10
Tìm hai số x,y thuộc N* biết rằng x.y=20 và BCNN(x;y)=10.
\(ƯCLN\left(x;y\right)=\frac{xy}{BCNN\left(x;y\right)}=\frac{20}{10}=2\)
Đặt \(x=2k,y=2t\) (y và t là 2 số nguyên tố cùng nhau)
\(xy=20\Rightarrow2k.2t=20\Rightarrow k.t=5\)
\(\Rightarrow k\inƯ\left(5\right)=\left\{1;5\right\}\)
\(\Rightarrow x=2k\in\left\{2;10\right\}\)
Nếu x = 2 thì y = 10
Nếu x = 10 thì y = 2
Vậy x = 2 và y = 10 hoặc x = 10 và y = 2
Tìm 3 số x, y, z biết \(\dfrac{x}{15}\)=\(\dfrac{y}{20}\)=\(\dfrac{z}{40}\) và x.y = 1200.
Đặt \(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{40}=k\Leftrightarrow x=15k;y=20k;z=40k\)
\(xy=1200\\ \Leftrightarrow300k^2=1200\\ \Leftrightarrow k^2=4\Leftrightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=30;y=40;z=80\\x=-30;y=-40;z=-80\end{matrix}\right.\)
Tìm hai số x ; y ∈ N * biết rằng x.y = 20 và B C N N x ; y = 10
Tìm hai số x,y thuộc N* , biết rằng x.y = 20 và BCNN(x,y) = 10
Tìm 3 số x, y, z biết \(\dfrac{15}{x-9}=\dfrac{20}{y-12}=\dfrac{40}{z-24}\) và x.y = 1200.