Cho ∆ABC vuông tại A , đường cao AH, biết AH=5cm,HC=2,5cm a,Tính HB b,Tính tấn của góc B Giúp!
H24
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm; BC = 5cm. a/ Tính AC, AH, HB, HC. b/ Tính các tỉ số lượng giác của góc B và tính góc C. c/ Vẽ HM vuông góc AB tại M; vẽ HN vuông góc AC tại N. Chứng minh: AM. AB = AN. AC.
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Đúng 0
Bình luận (0)
. Cho ∆ABC vuông tại A, đường cao AH. Tính độ dài HB, biết a) BC=5cm,AH= 6cm
b) AB=6cm,HC=5cm.
Câu b: AB^2=BH.BC=BH(BH+HC) =BH^2+BH.HC
thay số vào ta được HB=4
Đúng 0
Bình luận (4)
b) Ta có: \(AB^2=HB\cdot BC\)
\(\Leftrightarrow HB^2+5HB-36=0\)
\(\Leftrightarrow\left(HB+9\right)\left(HB-4\right)=0\)
hay HB=4(cm)
Đúng 0
Bình luận (0)
1. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB= 25cm, HC= 64cm. Tính AH, AC, góc B và góc C
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=40cm\\AC=8\sqrt{89}cm\end{matrix}\right.\)
Xét ΔACH vuông tại H có
\(\sin\widehat{C}=\dfrac{AH}{AC}=\dfrac{5}{\sqrt{89}}\)
\(\Leftrightarrow\widehat{C}\simeq32^0\)
hay \(\widehat{B}=58^0\)
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A đường cao AH= 2.4cm BC= 5cm
a,tính AB,AC,HB,HC
b,tính tỉ số lượng giác của góc C
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính góc B , C
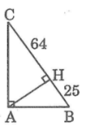
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
A H 2 = H B . H C
Suy ra:

Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, biết HB 9; HC 16. Tính góc B và góc C. A.
B
^
53
0
8
;
C
^
36
0
52
B.
B
^
36
0
52...
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH, biết HB = 9; HC = 16. Tính góc B và góc C.
A. B ^ = 53 0 8 ' ; C ^ = 36 0 52 '
B. B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
C. B ^ = 48 0 35 ' ; C ^ = 41 0 25 '
D. B ^ = 41 0 25 ' ; C ^ = 48 0 35 '
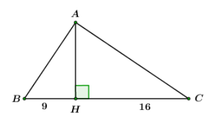
Ta có: BC = BH + CH = 9 + 16 = 25
Áp dụng hệ thức lượng cho ABC vuông tại A có đường cao AH ta có:
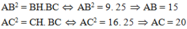
Xét ABC vuông tại A ta có:
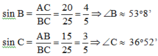
Đáp án cần chọn là: A
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH tia phân giác góc B cắt AC tại D . biết DA=2cm DC=3cm.
a) Tính góc B góc C
b) Tính độ dài của AH; HB; HC
a/ Theo t/c đường phân giác ta có : \(\frac{DA}{DC}=\frac{AB}{BC}=\frac{2}{3}\)
Trong tam giác vuông ABC có : sin C = \(\frac{AB}{BC}=\frac{2}{3}\)Từ đó tính đc góc C, góc B
Biết góc B, góc C tính được AB, BC
b/ Dùng các hệ thức tam giác vuông tính đc AH, BH, CH
Đúng 0
Bình luận (0)
Giúp mình với ak!!!!
1. Cho tam giác ABC vuông tại A, biết AB/AC=5/7 và đường cao AH=15cm. Tính HB, HC.
2. Cho tam giác ABC vuông tại A, có đường cao AH=14cm và HB/HC=1/4. Tính chu vi tam giác ABC.
1: AB/AC=5/7
=>HB/HC=(AB/AC)^2=25/49
=>HB/25=HC/49=k
=>HB=25k; HC=49k
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>1225k^2=15^2=225
=>k^2=9/49
=>k=3/7
=>HB=75/7cm; HC=21(cm)
Đúng 1
Bình luận (0)
cho tam gi1c vuông ABC vuông tại A đường cao AH, biết AH=4cm, HB=2cm, tính HC ,AB , AC , BC, góc B và góc C
Tam giác ABC vuông tại A , theo HTL :
AH^2 = HB .HC
=> 4^2 = 2 . HC = > HC = 16 : 2 = 8 cm
BC = HB + HC = 2 + 8 = 10
AB^2 = BH . BC = 2.10 = 20
=> AB = căn 20
AC^2 = HC . BC = 8 x 10 =80
=> AC = căn 80
TAm giác ABC vuông tại A
=> SIn B = AC/BC = căn 80 /10 => B = sin-1 ( căn 80 / 10) = 63 độ 26'
=> C = 90 - B = 90 - 63 độ 26 phút
Đúng 0
Bình luận (0)
Giải
Tam giác ABC vuông tại A , theo HTL :
\(AH^2=HB.HC\)
\(\Rightarrow4^2=2HC\Leftrightarrow HC=16\div2=8\left(cm\right)\)
\(\Rightarrow BC=HB+HC=2+8=10\)
\(AB^2=BH.BC=2.10=20\)
\(\Rightarrow AB=\sqrt{20}\)
\(AC^2=HC.BC=8.10=80\)
\(\Rightarrow AC=\sqrt{80}\)
Tam giác ABC vuông tại A
\(\Rightarrow\) SIn B = \(\frac{AC}{BC}\) = \(\sqrt{\frac{8}{10}}\)\(\Rightarrow\) \(B=sin^{-1}\) \(\sqrt{\frac{80}{10}}=63^026'\)
\(\Rightarrow C=90-B=90-63^026'\)
Đúng 0
Bình luận (0)



